disque
- 29
- 0
Homework Statement
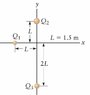
Three point charges Q1 = 2.9 mu or micro C, Q2 = 4.9 mu or micro C and Q3 = 3.9 mu or micro C, are arranged as shown.
Homework Equations
PE=k(q1q2/r+q1q3/r+q2q3/r)
k=8.99e9
The Attempt at a Solution
By using that equation I plugged in the lengths and changed the 2.9 to micro coulombs.