Calculating Pressure and Gravity Forces in a Two-Sphere System in Water

[Gh778]

I would like study a theoretical problem. A system composed of 2 spheres can move at left of at right in water. One sphere has gas at low pressure and other sphere has water in it. The wall of spheres are very thin and has the same density of water. Sphere of gas don't has force because it has same water at left and at right. But sphere of water "see" a virtual sphere of water that attract it (because in other direction there is sphere of gas), this force is F1. The pressure must compensate F1 but I don't understand how because pressure is give all around sphere of water and density is not a linear law and angles are not the same (if you change angle, you change distance).

And especially the layer around the sphere of water is not at R but at R more half thickness of molecule. Do you know if this calculation is done somewhere in the net ?

 

[Simon Bridge]

I don't understand your question.

The water-filled sphere with walls that have the density of water is basically an isolated lump of water. Therefore it floats in water at any depth. The buoyancy force is equal to the weight provided the sphere is totally submerged.

The air-filled sphere displaces it's own mass of water. Since this mass of water has a smaller volume than the sphere, the sphere will float with only part of it's volume submerged. If the sphere were totally submerged, then the buoyancy force on it would be the same as the buoyancy force on the water-sphere (provided they were the same volume)... i.e. equal to the weight of water displaced. The difference in behavior is because the buoyancy is not the only force at work here.

I think you will see the situation more easily if you use vertically oriented cylinders instead of spheres. The pressure of the fluid increases with depth - this means the pressure on the bottom of the cylinder is bigger than the pressure on the top creating a net force upwards. This is the buoyancy force.

I also suspect you'll benefit from Donald Simanek's treatment of buoyancy - which is in the context of the quest for perpetual motion (which helps explain the phenomena), making it more fun ;)
http://www.lhup.edu/~dsimanek/museum/themes/buoyant.htm
pmm can be a useful way of demonstrating physics - by counter-example.

 

[Gh778]

I'm interesting on the difference between attraction and pressure forces. If you let my study on Earth, supposed that gravity is exactly perpendicular to the image, like that it's easy to understand.

1/ Consider the sphere full of water: what are forces on it ? At right, gas attract near nothing in the contrary at left water attract sphere of water. For know the attraction, it's necessary to calculate all forces from one molecule of water at left on all molecules of water at right. Look at angles.

2/ Consider the pressure on sphere of water: what forces on it ? The pressure is given by the sum of all external molecules of the sphere.

Angles are not the same, so the distance not too, so the sum of force must be different (but it is equal), so I forget a force somewhere.

It's easier to calculate with square object like image is showing.

 

[Gh778]

I think you will see the situation more easily if you use vertically oriented cylinders instead of spheres. The pressure of the fluid increases with depth - this means the pressure on the bottom of the cylinder is bigger than the pressure on the top creating a net force upwards. This is the buoyancy force.

you're right it's easier to calculate:

On Earth, put a column of water on the ground. I put at top of the column a solid in water, with the same density of local water, the solid mustn't move. Pressure from Earth (gravity) give a weight to the solid and buoyant force from Earth attraction is the same force but at top (Archimedes). I'm agree with that.

But, I think water in the column attract molecules of water at top, between solid and walls of the column. For me there is another buoyant force (very small) due to the presence of water in the column. And I don't find the other force that canceled it. Why water in the column don't attract water at top ?

 

[Simon Bridge]

On Earth, put a column of water on the ground. I put at top of the column a solid in water, with the same density of local water, the solid mustn't move. Pressure from Earth (gravity) give a weight to the solid and buoyant force from Earth attraction is the same force but at top (Archimedes). I'm agree with that.

It is not useful to think of gravity as exerting a pressure. It is quite a different thing.

In order for the situation described to occur - the solid must be completely submerged.

And I meant that the solid should be considered to be a cylinder - not the body of water it is floating in.

But, I think water in the column attract molecules of water at top, between solid and walls of the column.

You mean the surface tension?
Like you get a meniscus due to the attraction of the liquid to the sides of the container or whatever?

For me there is another buoyant force (very small) due to the presence of water in the column. And I don't find the other force that canceled it. Why water in the column don't attract water at top ?

I don't understand the question - all the water is attracted to all the water all the time but there is no special affinity of water for water.

Perhaps you are wondering why water doesn't just all get squashed at the bottom of the container - compressed under it's own weight? The answer is that it does - that's what you see. The force holding the water up as a column is electrostatic. That is what causes the pressure difference with depth.

 

[Gh778]

And I meant that the solid should be considered to be a cylinder

it's easier, yes the solid is in water. I think it's possible to think in 2d.

You mean the surface tension?

not at all.

I don't understand the question - all the water is attracted to all the water all the time but there is no special affinity of water for water.

I think it's that I don't understand. Take a molecule at top between wall and solid. What forces on it ? From Earth and from water behind it, no ? For me the column add additional gravity, not ?

Edit: don't forget gravity change with 1/d² in the column too, it's very important because a molecule at bottom of the column has more force to the center of Earth than a molecule at top. When a molecule at top attract molecule at bottom, it's not a mass with a mass, it's a weight with another weight. For me, the pressure at bottom decrease and the pressure increase around the solid. Another point, gravity force from Earth is very big compared than attraction of molecule/molecule in column, so this is not like in space. I lost something ?

 

[Gh778]

I understood, no additional force for solid due to the presence of water in column. The same for water on water (buoyancy), all forces cancel themselves on the last case.

I have 2 anothers questions:

1/ Study 1

a/ Put a solid (height = 1 m, same density than liquid in column) at 11 m of altitude, the weight is P1
b/ Now, put below the solid a column full of water (height of the column = 10m), the weight of solid is now P2 with P2>P1 because water attract more solid (solid is not in water)
c/ Move down the solid of 1m (solid is in water), what is the weight ? I thought it is near P2 but if water don't attract solid when it is in water, the weight is P1 ?

2/ Study 2

Look at the image, it's the top of the column with a solid in it. Molecules of water attract each others. This don't increase Archimedes law ?

 

[Simon Bridge]

I understood

Somehow don't think you did, because you go on to ask:

a/ Put a solid (height = 1 m, same density than liquid in column) at 11 m of altitude, the weight is P1
b/ Now, put below the solid a column full of water (height of the column = 10m), the weight of solid is now P2 with P2>P1 because water attract more solid (solid is not in water)

What makes you think the water has a special attraction for the solid that it does not have for other water? Where is this idea coming from?

Are you thinking of gravitational attraction here?
Please be clear.

c/ Move down the solid of 1m (solid is in water), what is the weight ? I thought it is near P2 but if water don't attract solid when it is in water, the weight is P1 ?

What attraction are you talking about?

Note: the weight of the solid is defined to be "the strength of the gravitational force on it".
Close to the surface of the Earth, with objects very small compared with the Earth, the weight is approximately constant. You do get small variations depending on the local distribution of mass though.

The weight of an object sitting next to a swimming pool is technically going to change a bit when you put it in the swimming pool because there are different mass distributions around it - it's got closer to the Earth's core by the depth of the pool (if it sunk) for eg. But that difference is so miniscule it is safe to ignore it - you can have a go calculating it. None of your scales will be able to measure the difference.

2/ Study 2

Look at the image, it's the top of the column with a solid in it. Molecules of water attract each others. This don't increase Archimedes law ?

How are the molecules of water attracting each other? What are you talking about here?

Any mysterious attraction forces would contribute to the pressure of the liquid - so I doubt there would be any need to alter the calculation. You do need to alter the calculation for surface tension - which is important for very small objects.

I'm sorry - nobody can help you if you won't say what you are talking about.

 

[Gh778]

What makes you think the water has a special attraction for the solid that it does not have for other water? Where is this idea coming from? Are you thinking of gravitational attraction here?
Please be clear.

Yes, I speak about gravitationnal attraction. I know water attract solid or anything else but I don't understand the difference of weight when an object is in water or not, (it must be the same, ok) take this case:

1/ On Earth, a solid is placed at 100,001 km of altitude, at this altitude the weight is P1 (I don't care about the precise, it's just P1 value and I ignore gas). Solid is 1 m of height.
2/ I put a column of water (height 100 km) under solid, the water attract solid, true ? so the weight is not P1 but a little more: P2
3/ I move down the solid of 1 meter in water, the weight must be a little below P2 (-1 m), true ? but when solid is in water how water can do for attrack solid in water ? Could you explain this point ?

How are the molecules of water attracting each other? What are you talking about here?

A molecule attract any other molecule in water, no ? when a solid is put in water, molecules at right attract molecules at bottom, and molecules at left attract molecules at bottom. The solid is between molecules, there is a force on it, no ? They can't attract at top, there is no water. Lateral forces cancel themselves. But I see a up force and I don't know how Archimedes law take in account this because it depend of the shape, number molecules at sides.

 

[russ_watters]

Archimedes Law does not take into account the gravitational force of the water molecules on each other because those forces are insignificantly small.

 

[Simon Bridge]

In buoyancy, gravitational attraction of everything for everything else is completely accounted for by the weight of the object and the pressure of the water.

The weight of the object includes the gravitational force exerted between the object and the water.
The attraction of the water to itself as well as to the Earth, the walls of the container etc, is what gives rise to the difference in water pressure with depth.

The difference in water pressure with depth is what gives you the buoyancy force.

Archemedes Law - as you find in textbooks, would need to be altered slightly to allow for this sort of thing but, as russ_watters points out, the correction is extremely tiny. You will never encounter a situation where it matters.

Similarly - water molecules will have electrostatic forces on each other (which are much much bigger than the gravitational forces btw) and those don't have much effect either. Water is also not usually pure H₂O - and the impurities may change the effect. This is a bigger effect as well, but the biggest effect the impurities will have is in changing the average density of the water so Archemedes law will still hold.

 

[Gh778]

Archimedes Law does not take into account the gravitational force of the water molecules on each other because those forces are insignificantly small.

Ok, I don't knew ! thanks !

For my last message, #9 step3, the weight at step 3 is P1 or P2 ? If it's P2 could you explain how water can do for attract solid in it ? Because, solid attract molecules of water but they are in contact with solid and the force is canceled, no ?

I know the force I speak is very small but I want to understand how this works in reality

 

[russ_watters]

Sorry, I still find your messages mostly incoherent.

 

[Simon Bridge]

Sorry, I still find your messages mostly incoherent.

That's OK I got it. Gh778 is struggling to express himself in English - a matter exacerbated by being unfamiliar with the terms. I think I got it...

Ok, I don't knew ! thanks !

For my last message, #9 step3, the weight at step 3 is P1 or P2 ? If it's P2 could you explain how water can do for attract solid in it ? Because, solid attract molecules of water but they are in contact with solid and the force is canceled, no ?

I know the force I speak is very small but I want to understand how this works in reality

I think you need to be more careful with your words - they don't actually mean what you appear to think they do.

Per you last message #9 - let's take them in order:

1/ On Earth, a solid is placed at 100,001 km of altitude, at this altitude the weight is P1 (I don't care about the precise, it's just P1 value and I ignore gas). Solid is 1 m of height.

The weight of the object is, by definition, the force of gravity on the object.
That value is given by Newton's Law of Gravitation thus:

$$P_1=\frac{GMm}{(R+A)^2}$$... where R is the mean radius of the Earth at sea level, and A is the height above sea level (the usual meaning of "altitude"). M is the mass of the Earth, and G is the gravitational constant. You can look up all those values and do the math yourself.

... if we use distance in km then G=6.67x10^-17 km³kg^-1s^-2.

... M_E=5.972x10²⁴kg

... let's make the test mass an even 1kg

... R=6371km

... A=100,001km is very high indeed - it's about a third of the way to the Moon's orbit.

You probably mean that r=R+A=100001km but what you said was "altitude" so I will take you at your word, so the center of mass of the object is r = R+A = 106372km away from the center of mass of the Earth.

Is this object in free-fall by any chance? i.e. what is keeping it there?

2/ I put a column of water (height 100 km) under solid, the water attract solid, true ? so the weight is not P1 but a little more: P2

OK - you take a bit of the Earth (where else would the water come from?) and move it closer.
The column is h=100km high and has a mass M_w (you really needed the other dimensions) so it's center of mass is (r-h/2)km away from the center of the Earth, which is 50km away from our object... and the Earth mass has decreased by $M_w$ and the calculation becomes:
$$P_2=\frac{G(M-M_w)m}{(R+A)^2}+\frac{4GM_wm}{h^2} > P_1$$

There is a 4 in the second term because there was an (h/2)² in the denominator.
Note - we could imagine the column of water is a cylinder with end-surfaces of 1km² areas - so the overall volume of the water is V_w=100km³ ... which sounds like a lot, but the Earth has 1385920460km³ available :)

OK. What I want you to do is calculate how much bigger P2 is from P1 as a percentage.

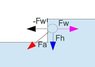
3/ I move down the solid of 1 meter in water, the weight must be a little below P2 (-1 m), true ? but when solid is in water how water can do for attrack solid in water ? Could you explain this point ?

When the solid is a short distance d below the surface of the water, it's altitude is now A-d, and there is a column of water height d above it. The water above it attracts the mass upwards - so now we have three terms in the calculation.

$$P_3=\frac{G(M-M_w)m}{(R+A-d)^2}+\frac{h-d}{h}\frac{4GM_wm}{(h-d)^2}-\frac{d}{h}\frac{4GM_wm}{d^2}$$ ... again, you can crunch the numbers: this means that $P_3<P_2$Those (h-d)/h and d/h terms are because the mass of water below the object is (h-d)M_w/h and the rest is above it.I suspect you want to try to apply these calculations to Archimedes next.
For that you have to be a lot more careful with your setup - if the water and the solid object are both in free fall, that will affect your calculation. Archimedes is kinda assuming that the container for the water is sitting on the ground.

Archimedes also kinda assumes that things are happening on a smaller scale.
With very big volumes - water is not really un-compressible, for example.
Gravity is no longer uniform - there are tidal effects - stuff like that.

Lesson: Archimedes is good on the scale of bathtubs and crowns.
For other stuff, you may just have to add up all the little contributions... which means calculus.

 

[Gh778]

Sorry, it's not 100001 km, it's 100 km +1 m = 100.001 km :( it is altitude, like that when I put a column of water of 100 km height the solid is just above.

The diameter (or square section) of the column is only 1 m, this could change the center of mass of Earth ? If yes, for simplify the study, it's possible to add another column of water at opposite diameter ? like that this don't change the center of mass of Earth. It's easier for me to understand if Earth don't move.

For me, and if I take your equations:

1/ at 100 km +1 m the solid has P1 weight
2/ I add 2 columns of water diametrically opposed on Earth, height of column = 100 km, the solid is outside water, the solid has weight P2
3/ I move down object of 1 m it is full in water, now, what is the weight, it is P1 or P2 ?

and thanks to take your time and try to explain even my english is bad :)

 

[Simon Bridge]

3/ I move down object of 1 m it is full in water, now, what is the weight, it is P1 or P2 ?

niether.
I urge you to do the calculations yourself.

 

[Gh778]

I don't know, for me it's P1 because additional water don't attract solid when it is in water, I don't want the exact value, I just want to understand what's happen when solid is move down of 1 meter, the weight must be the same P2 (at 1 meter near), but like molecules of water touch walls of the solid for me molecules of water can't attract solid so the weight is only the weight from Earth like if column of water is not there.

 

[Simon Bridge]

I told you - it's neither.
Gravity works all the time - it does not magically switch off when you are under water.

 

[Gh778]

Archimedes Law does not take into account the gravitational force of the water molecules on each other because those forces are insignificantly small.

Ok, you accept these forces. So with a shape like that in water, on Earth, red object move alone at left ? Even there is viscosity the lateral force must be 0 (you can replace water by helium).

 

[russ_watters]

Ok, you accept these forces. So with a shape like that in water, on Earth, red object move alone at left ? Even there is viscosity the lateral force must be 0 (you can replace water by helium).

No, it does not move. We've discussed this exact issue many times.

 

[Gh778]

Ok, so in this case red forces don't exist ? Atoms of helium don't attract atoms of helium through volume of gas ? Why ? The volume of gas is asymetric and I don't understand why sum of red forces can be at 0. At right there are red forces, not at left (no helium at bottom). Someone in this world has computed this for test or test in a container of helium ?

 

[russ_watters]

What is a "red force"?

In this example, it is easy to see that the surface area facing left and the surface area facing right are equal, so the forces pushing in each direction must be equal.

Also, gas molecules don't attract each other, they repel each other; that's what creates the pressure. Regardless of that, buoyancy works the same in a gas and liquid.

 

[russ_watters]

That's OK I got it. Gh778 is struggling to express himself in English - a matter exacerbated by being unfamiliar with the terms. I think I got it...

A language barrier does not prevent one from being able to make quality drawings. I think the communication issue is more fundamental than just language.

 

[Gh778]

What is a "red force"? In this example, it is easy to see that the surface area facing left and the surface area facing right are equal, so the forces pushing in each direction must be equal.

Red force is gravitational force: a mass attract a mass, so an atom of helium must attrack an atom of helium, the force is very small. The surface at right = surface at left, I'm agree. But at left: atoms of helium can't attract atoms of helium through walls of solid.

Also, gas molecules don't attract each other, they repel each other; that's what creates the pressure. Regardless of that, buoyancy works the same in a gas and liquid.

It's a liquid helium not a gas, low temperature, no friction.

A language barrier does not prevent one from being able to make quality drawings. I think the communication issue is more fundamental than just language.

Sorry, for my poor english. I try to explain the best I can.

 

[russ_watters]

Red force is gravitational force: a mass attract a mass, so an atom of helium must attrack an atom of helium, the force is very small. The surface at right = surface at left, I'm agree. But at left: atoms of helium can't attract atoms of helium through walls of solid.

1. We already explained that the gravitational force between helium atoms is insignificant. You should calculate it to prove to yourself it is.
2. In your sketch, the force lines you draw go through the object.
3. The lines are not perpendicular to the object.

 

[Gh778]

1. We already explained that the gravitational force between helium atoms is insignificant. You should calculate it to prove to yourself it is.

Even if one atom attrack one atom, the force can be like 1e-60 N, it's very small, but sum of force must be exactly at 0 and if liquid helium has no viscosity this would say the object can accelerate with this force.

2. In your sketch, the force lines you draw go through the object.

Yes, why not ? the gravitational attraction is direct (line from atom A to atom B), no ? I put gas at low pressure in white object, low pressure that it's possible to have.

3. The lines are not perpendicular to the object.

Ok, but a part of force is apply to the surface of object (-Fw in vector), object apply a force perpendicular (Fw) to its surface on the atom of helium and a rest of force is for atom of helium (Fh). For me, atom of helium move down and object move at left. What's wrong ?

 

[Simon Bridge]

Even if one atom attrack one atom, the force can be like 1e-60 N, it's very small, but sum of force must be exactly at 0 and if liquid helium has no viscosity this would say the object can accelerate with this force.

No - because the sum of all the forces are exactly zero. The very small gravity force means that the other forces are very slightly different from the usual approximation as well.

Ok, but a part of force is apply to the surface of object (-Fw in vector), object apply a force perpendicular (Fw) to its surface on the atom of helium and a rest of force is for atom of helium (Fh). For me, atom of helium move down and object move at left. What's wrong ?

Did you include every force.

You have to sum all the forces. There are lots of them and if you insist on including every single insignificant force as well all you'll get is a very big summation that still comes to zero.

Gravity should be acting at the center of mass while pressure forces should act perpendicular to the surfaces. Don't forget that every action has an equal and opposite reaction.

Dealing with these sorts of ideas by looking at forces can be confusing.
You should also check your ideas by looking at conservation of energy - if the object were to accelerate, it would gain energy - where did that energy come from? How did it get there?

BTW: you seem to have abandoned your previous question and moved onto something else.
But you don't seem to be applying the lessons from previous posts and other threads to the new subject. The lessons are applicable - do use them.

 

[K^2]

Am I the only one who thinks that picture in the first post presents a very cool problem? If we assume that there is no external source of gravity, only water, then the g-field is as OP described. It's going to pull the water-filled sphere to the left, away from the air-field sphere. In contrast, there is no net force on the air-field sphere. So the question is why two spheres don't move together to the left.

And, of course, the answer is pressure. The problem is that OP drew that also to the left, but pressure is going to push the water-filled sphere to the right. Why? Because the air-field sphere placed in an infinite pool of water is going to behave like an object with negative mass. It's going to repel all the water around it. And if we take water to be perfectly incompressible, then a pressure gradient will establish to keep all water static. That pressure gradient is going to push on water at every point in this pool towards the air-filled sphere with the force exactly opposing gravity. That includes the water-filled sphere.

So the problem is static, nothing is going to move, obviously. It's just much easier to see if you take air-filled sphere as the center of everything and consider the g-fields from that perspective.

 

[Simon Bridge]

Am I the only one who thinks that picture in the first post presents a very cool problem? If we assume that there is no external source of gravity, only water, then the g-field is as OP described. It's going to pull the water-filled sphere to the left, away from the air-field sphere. In contrast, there is no net force on the air-field sphere. So the question is why two spheres don't move together to the left.

It could be any number of intriguing puzzles depending on how one reads the diagram.
The main trouble is that it is not at all clear what is intended.
Notice how the diagram changes is the wall of the water sphere is made a bit bigger?
Asked to be clearer, OP just changed to a different setup.

 

[K^2]

The description of the diagram seems pretty clear, once you get over the broken English. The thickness issue comes up only because OP is a bit confused on how the relationship between pressure and buoyancy works.

 

[Simon Bridge]

Well it is neat.

 

[Gh778]

Asked to be clearer, OP just changed to a different setup.

If I changed some parameters in the problem it's because I try to find the best problem (easier to resolve), it's not easy.

No - because the sum of all the forces are exactly zero.

Ok, in this case it's possible to show me another forces which compensate red forces. Not compute just drawing it.

It could be any number of intriguing puzzles

You have to sum all the forces.

I would like to simulate forces with only gravity attraction law (1/d²). If the system is small it's possible to compute with a program, a 2d problem with only one layer of molecule for the thickness, N-body simulation can do that, but for take all parameters like density it's difficult to do for me, not for you I think. Someone to start the problem ?

Am I the only one who thinks that picture in the first post presents a very cool problem?

Because the air-field sphere placed in an infinite pool of water

Simon will say I changed the problem again but it's possible to put it in a disk. No infinite water.

while pressure forces should act perpendicular to the surfaces

I hope nobody will burn me but I'm not agree with you. If I consider only pressure force from external gravity pressure, ok, I'm right with you. But if I consider attraction from others particles through the object to study, for me I don't see that like perpendicular, if object is asymetrical how pressure force can be perpendicular ? An example (not another case), Fp is perpendicular but attraction from another particles through object give Fr, the sum of forces are not perpendicular. Sure, the difference is very small, but physics must take it in account. So, another force ?

 

[K^2]

Simon will say I changed the problem again but it's possible to put it in a disk. No infinite water.

Doesn't matter. So long as the air-field sphere is at the center of relevant symmetries. In other words, if air-filled sphere is at the center of the cylindrical pool of water, all of the logic I stated applies. The pressure gradient still establishes as stated, and the gravitational force on the water-filled sphere will be balanced by said pressure gradients.

 

[Gh778]

You compute the density is different due to the presence of air-filled sphere ? Inside water-filled sphere the density is not the same than at external.

 

[K^2]

The assumption is that water is incompressible. So density is exactly the same everywhere, except for where water is replaced with air. There, obviously, density is less.

The field configuration will depend on choice of the shape for the pool of water. For example, in spherical pool, gravity will point inward everywhere and be zero inside the air-filled sphere.

But in absolutely any of these cases, you will end up with pressure gradient establishing that prevents water from flowing. That will also be the pressure gradient that keeps the water-filled sphere put.

There is absolutely nothing magical about this setup. It has a well-behaved equilibrium state.

There is, of course, question of stability in a finite pool. For example, I strongly suspect the equilibrium with air-filled sphere to be unstable. So if it's just a bit off-center, the air-filled sphere will "surface" to the edge of the pool.

 

[Gh778]

The assumption is that water is incompressible.

I said that ? For me water is compressible. You can change water by liquid helium at low temperature. Compressibility of liquid helium is bigger (100 times more than water I think).

 

[K^2]

You could. It would make the problem numerically more complex and won't change the answer. You are still dealing with something that's completely static due to symmetries. So you'll still have pressure gradients that keep everything from moving.

 

[Gh778]

Have you seen image in message #32 ? How force from pressure can be perpendicular with a simple asymmetrical object ? For me, particle attrack particle through object.

 

[K^2]

We can't discuss an infinite set of problems due to there being infinitely many. You've had a specific definition in your first post. We've covered all possible variations there of. Gravity and pressure balance there.

If you have a different problem, it's a different problem. But you should be working it out the same way. There is only going to be motion if it's going to reduce system's energy. If you start out at the minimum, there will not be any movement. And it's not hard to come up with simple examples that are out of balance. Place a sealed container with air under water and let it go. It comes up to the surface, because that minimizes energy.

If you think you see a situation where you expect motion while energy of the system isn't changing, look for a mistake. That's all there is to it.

 

[Gh778]

It's not infinite set of problems, just 2 cases, first I would like study internal/external attraction forces like first post say, second I would like to study attraction of particles through object itself. I think these problems are link if I want to understand all pressure/force. Look image in message #24, what force cancel red force ?

I would like to compute sum of forces on object (that can move or turn) with only gravitationnal attraction forces. I saw N-body simulation but it's for free object. How can I apply this sort of simulation with my examples ? I would like to take in parameters the density of liquid. Someone can help me to do this ?

 

[Simon Bridge]

I said that ? For me water is compressible.

You said it when you specified "water" i your setup - and you seemed to want the simplest model.
http://ga.water.usgs.gov/edu/compressibility.html
... you intended a compressible liquid?

Don't get me wrong - I'm not complaining about the parameters of the problem changing - I was explaining why I, for one, didn't dwell on the initial diagram.

You can change water by liquid helium at low temperature.

Very low temp.

Compressibility of liquid helium is bigger (100 times more than water I think).

Or, indeed any compressible fluid. And you can replace the "air" with any low density fluid.
You understand that things float in air right?

All the arguments prev still hold - the compression of the gas makes them a bit more complicated but the low-density volume acts like an absence of mass with the exact result depending on the geometry of the various elements.

i.e. if you had a large ball of compressible fluid with no external gravitation, then we have to ask why it stays as a ball right? Maybe it is held together under it's own gravitation? Well then the density will vary with radius, most dense at the center.

So the equivalent problem would be to have an enclosed void in the ball right next to an enclosed volume of the same fluid at the same distance from the center. Or, maybe, you have one at a greater radius than the other.

The voided sphere will want to rise of course - head away from the center of mass. It's less dense that the surroundings and the pressure gradient is reinforced by a density gradient.

Or, maybe, you want the classical infinite volume of fluid all at a constant temperature? In that case the density is initially equal everywhere since there is no center - so is the pressure. But if we put an enclosed void someplace, that place automatically becomes a center and then we now have an asymmetry.

If I remember my cosmology properly, the thing with infinite uniform mass distributions is that small asymmetries cause things to move about - the compressible fluid collapses over time - it's no longer a static system.

I don't want to go further without checking with you for what you are talking about.

But K^2 is correct - you need to work the energy description - what will reduce the energy.
Trying to work the forces will just get you confused and it is better than continually coming up with more and more examples ... there are always more, it's the nature of knowledge. Look for ways to group them into classes of problems and solve them like that.

 

[Gh778]

you intended a compressible liquid?

yes, it's very important when the study is in a disk.

Very low temp.

sure, but it's not a problem. I saw in particular liquid helium has no viscosity.

You understand that things float in air right?

I don't understand (english)

But K^2 is correct - you need to work the energy description - what will reduce the energy.

I prefer compute with forces that I know.

you want the classical infinite volume of fluid all at a constant temperature? In that case the density is initially equal everywhere since there is no center

That the heart of the problem, I study attraction forces from liquid particles to liquid particles itself through an object. If the study is on Earth, this don't change the problem if study is perpendicular to Earth's gravity. I prefer to study on Earth because in space I need to study with big dimensions and need a long time to compute.


The best I can do is to compute with a program and understand how forces are in equilibrium state. Like I described a study, someone can help me to compute it ? I would like to compute torque of object around black disk.

 

[Gh778]

I think I understood where is my problem. I change the study: it's a solid torus with 2 solid balls in it like drawing show. Balls attrack each others with a spring. If I done sum of forces, I can see sum of forces on each ball is 0. For the torus too, but red forces don't apply at the same radius and I see a torque. Could you explain the error I done ?

 

[Simon Bridge]

sure, but [super-cold] not a problem. I saw in particular liquid helium has no viscosity.

Liquid helium introduces all sort of odd effects.
But we can figure for a compressible, negligible viscosity, fluid without specifying the actual material - since we are just making models.

I don't understand (english)

"fluid" does not have to mean "liquid" - gasses are fluids too. Buoyancy rules work for gasses as well.

I prefer compute with forces that I know.

Which just makes it harder for yourself.
In very complicated systems the forces can get quite subtle and they stop being a useful way of analyzing things.

That the heart of the problem, I study attraction forces from liquid particles to liquid particles itself through an object. If the study is on Earth, this don't change the problem if study is perpendicular to Earth's gravity. I prefer to study on Earth because in space I need to study with big dimensions and need a long time to compute.

Earth's gravity will still affect everything - for instance, the gravity will create a vertical pressure gradient in a fluid. If the fluid is compressible, then there will be a density gradient as well.

 

[Simon Bridge]

Looking at your diagrams - it would help if you told me what it is that these studies are supposed to help you with?
What is the problem you are trying to solve?
Because it looks like you are trying to build a perpetual motion machine.

The first one with the liquid helium is meaningless to me - I cannot tell what the parts are supposed to be.
The second one with the solid torus...

Are you still trying to understand gravity?
The gravitational field of a torus is a little difficult.
Your two solid balls inside cavities in the torus are pulled towards each other by the spring - and also by each other's gravity. They also experience the torus' gravity and any external gravity fields.

Why the spring? What is ti supposed to show?
Why a torus? Is the torus supposed to be spinning?
Anyway - in the configuration shown, everything is held static by the spring.

If the red arrows are indicating gravity from the block of solid they point at, then you seem to have forgotten the gravity from the solid material in the other direction. You have to sum all the forces. Gravity acts between centers of mass. All the torus affects the spheres.

The center of mass of the torus is slightly off-center because of the holes the spheres are sitting in but both spheres will try to get closer to that point which will be close to the center of the torus.

 

[Gh778]

no gravitational forces here ! just a spring that can be attact 2 balls. the solid can only turn. I done sum of forces and for me red forces don't apply them with same radius, so I see a torque.

 

[Simon Bridge]

If there is no gravity - then the free-body diagrams for each sphere will have the spring force pointing along the line of the spring and two reaction forces from contact with the two solid surfaces.

The balls are being held against a corner by the spring... add in the forces from the walls.

 

[Gh778]

just for understand the "thing" I don't understand with particles, gravitational attraction is like a spring in fact. With 2 balls it's easier to understand. Why red forces don't apply a torque ?

 

[Simon Bridge]

I think I can see how you are thinking here ... the tangential components of the spring force on each ball pushes the balls against the walls at different radii - so they apply a different torque. You have to remember that the walls push back which, in that analysis, will produce a net counter-torque the same size.

The balls are being held against a corner by the spring... add in the forces from the walls.

 

[Gh778]

but sum of force for each ball is 0, and the wall apply counter force to the ball not on itself, I don't understand