xayon
- 3
- 0
Homework Statement
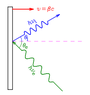
A mirror is moving uniformly in a direction normal to its plane with velocity v=βc. Given the angle of incidence and frequency of an incident photon (θ_e,nu_e in the figure), calculate the reflection angle and the observed new frequency (θ_i,nu_i in the figure).
Also prove that:
sin(θ_e)/(1+βcos(θ_e)) = sin(θ_i)/(1-βcos(θ_i))
Homework Equations
It has been suggested in a couple of threads to use Lorentz transformations, but i seem to have problems dealing with them.
The Attempt at a Solution
As said, my attempts to use them have been an utter failure. In the mirror's system the angles should be the same, but i get stuck at this point.