Calculating Ring Capacitance: MKS Units & Math Involved

[Saitama]

I was reading the following thread at stackexachange.
http://physics.stackexchange.com/qu...e-electrostatic-force-does-wire-thickness-mat

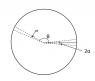
The first answer calculates the radial force using the capacitance of ring. Any ideas how the poster derived the formula for capacitance? Is the formula different for MKS units? I am interested in deriving it if it doesn't involves too much of mathematics.

Any help is appreciated. Thanks!

 

[gneill]

Nasty math including complete elliptic integrals, toroidal functions, and recurrence relations; see:

The Capacitance of an Anchor Ring

 

[Saitama]

Nasty math including complete elliptic integrals, toroidal functions, and recurrence relations; see:

The Capacitance of and Anchor Ring

Nope, I definitely cannot understand that. Does the formula remains same in MKS unit?

Btw, I am much more interested in calculating tension in the ring. I tried calculating force on a single particle which subtends a very small angle of $2\alpha$ at the center. The charge on this small part is $\lambda R (2\alpha)$ where $\lambda$ is the linear charge density and R is the radius of ring. It is obvious that that the force on this small particle is horizontal in direction (along the radius R). Consider another particle subtending angle $d\theta$. Charge on this is $\lambda (Rd\theta)$. The force due to second particle on first is
$$dF=\frac{k\lambda^2 R^2 2\alpha d\theta}{r^2}$$
where $r^2=4R^2\sin^2(\theta/2)$ (calculated from the law of cosines).
Integrating the component along the horizontal direction i.e integrating $dF\sin(\theta/2)$
$$F=\int_0^{2\pi} \frac{k\lambda^2 R^2 2\alpha d\theta}{4R^2\sin (\theta/2)}$$

But wolframalpha says that its not possible to calculate the above integral.

Thank you!

 

[haruspex]

$$F=\int_0^{2\pi} \frac{k\lambda^2 R^2 2\alpha d\theta}{4R^2\sin (\theta/2)}$$

But wolframalpha says that its not possible to calculate the above integral.

It clearly diverges near θ=0. This is not uncommon when treating charge as distributed on an infinitely thin wire. In reality, wires have thickness, and this becomes important at close quarters between the two regions of charge being considered in the integral. A possible way around it is to use a different approximation for that part of the integration where the two elements are within a distance equal to the wire's thickness, or thereabouts.