chawki
- 504
- 0
Homework Statement
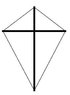
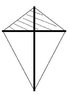
The lengths of the two perpendicular supporting rods are 80.0cm and 105.0 cm. The lengths of the two shorter sides are 50.0 cm and the lengths of the two longer sides are 85.0cm.
The supporting rods are drawn with a bolded line in the figure.
Homework Equations
Calculate the area of the kite in the figure and give the answer in units meters squared.
The supporting rods are drawn with a bolded line in the figure.
The Attempt at a Solution
we divide the kite into two triangles, the up triangle and lower triangle
Akite=Aup+Adown
Aup= 0.8*0.3/2 = 0.12m2
Adown= 0.8*0.75 / 2 = 0.3m2
Akite= 0.12+0.3 = 0.42m2