- #1
SteveDavies
- 3
- 0
- TL;DR Summary
- Two rectangular magnets, each of 1 Tesla, are spaced 3cm apart, with their large areas facing each other - North facing South. How do I find the flux density at the point between them?
This is for an experiment to deflect a 28 SWG wire between two magnets, 3cm apart, by passing a current through it (example attached). The force on the wire is obviously F = BIL, but the wire will be passing at 1.5cm from each magnet so there will be some significant fall off of B and I can't assume B (in BIL) to be 2 Teslas. The magnets are 5cm × 1.9cm × 0.6cm and 1 Tesla each.
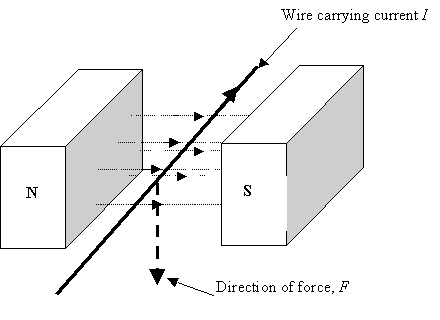
Many thanks,
Steve.
Many thanks,
Steve.