Calculating the intersection of a branching point

In summary, the conversation discusses the difficulty in calculating the volume of a complex geometric shape, specifically the fork of a tree. The shape consists of a conical segment that splits and merges into two smaller conical segments, and the volume of the internal space needs to be calculated using length, radius, and angle measurements. The diagram attached provides a better understanding of the shape. The person is stuck on calculating the volume between the three segments due to the varying sizes and angles. They suggest a potential solution of dividing the intersecting space into four segments, but are open to other suggestions. One suggestion is to model the shape after a soap film attached to three circular openings. Another suggestion is to use a frustrum of elliptical section to connect the
  • #1
MattRNR
1
0
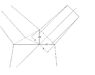
I am having trouble calculating the volume of an unconventional and variable geometric shape (the fork of a tree). I have a conical (frustum) segment which splits and merges at the smaller end into the larger end of 2 smaller conical (frustum) segments and need to calculate the volume of the internal space (using only the length measurements (for each conal frustum), radius measurements (for all 3) and angle measurements (between the middle lines of each of the 2 splitting conal frustums). A diagram (Branching Point) of this should be attached and will make significantly more sense than i do... (Note: i realize in the diagram my radius measurements are a bit displaced but i have the distance of these from the end points and can account for this with a little trigonometry)

Where I am stuck is calculating the volume of the area between the 3 segments, which is infuriating enough on its own, however is further complicated by the problem that (much like the branch of a tree) the two segments may not be the same size nor will the angle between the two segments be constant. Any resultant calculations will have to accommodate for these variables by incorporating them into the equation.

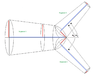
I really am quite stuck here, calculating the volume for each of the conal frustums individually is relatively straight forward, wherein volume can be calculated as [{((π*L)/3)*(R squared + (R*r) + r squared)} where V = Volume, L = Length, R = the largest radius and r = the smallest radius], however for the space in between I'm drawing a blank. The only strategy i can think of is to calculate the volume of the intersection using 4 segments each consisting of a conal frustum that is divided by 2 (this should make more sense in the diagram also (CF method)).

any help you could provide would be greatly appreciated.
 

Attachments

  • CF method.png
    CF method.png
    10.2 KB · Views: 479
  • branching intersection.png
    branching intersection.png
    31.9 KB · Views: 515
Mathematics news on Phys.org
  • #2
There's no obvious definition for what the shape is, let alone its volume.
A natural choice might be the shape that would be taken by a soap film attached to the three circular orifices. That would give the least area, so may be quite treelike, but the equations for those can be quite nasty.
Another choice would be to connect each smaller orifice to its parent by some sort of frustrum of elliptical section, then take the union of the two.
 

FAQ: Calculating the intersection of a branching point

What is the purpose of calculating the intersection of a branching point?

The intersection of a branching point is calculated in order to determine the location where two or more branches of a network or system meet. This information is useful in understanding the connectivity and flow of the network, as well as identifying potential sources of problems or inefficiencies.

What factors are taken into account when calculating the intersection of a branching point?

The calculation of the intersection of a branching point takes into account the position and direction of each branch, as well as any physical barriers or constraints that may affect the flow of the network. Other factors such as the size and capacity of each branch may also be considered.

What methods or tools are commonly used for calculating the intersection of a branching point?

There are several methods and tools that can be used to calculate the intersection of a branching point. These include mathematical equations, computer simulations, and physical modeling. The specific method used will depend on the complexity and accuracy needed for the particular network or system.

How does the calculation of the intersection of a branching point impact real-world applications?

The calculation of the intersection of a branching point has practical applications in a variety of fields such as transportation, telecommunications, and urban planning. It can help optimize the flow of traffic, improve network efficiency, and identify potential problem areas.

What are some limitations or challenges in calculating the intersection of a branching point?

One challenge in calculating the intersection of a branching point is accurately representing the real-world conditions and variables in a theoretical model. Additionally, the complexity of the network and the number of branches can make the calculation more difficult and time-consuming.

Similar threads

B Calculating 'Typical' Grade of a Hiking Trail
Replies
5
Views
2K
I Calculate new height of truncated cone
Replies
4
Views
2K
Intersection of two line segments from uniform distribution
Replies
17
Views
2K
Working out a point / segment on a sphere
Replies
3
Views
2K
MHB Formula for changing a plane intersection angle
Replies
3
Views
2K
Calculate all mid points of a line at a given interval
Replies
4
Views
2K
I Volumes of n-Spheres: Intuition & Calculations
Replies
8
Views
2K
I Ave length of intersection of all lines through a unit cube
Replies
4
Views
2K
I Relationship between the radius and area of liquid in a cylinder
Replies
6
Views
2K
MHB Find the distance between points C and D if the height of the tree is 4m
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top