Rahulrj
- 107
- 0
Homework Statement
To calculate moment of inertia of a solid sphere of uniform density[/B]
Homework Equations
$$ I = \int r^2 dm$$
The attempt at a solution
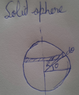
I consider an elemental disk of small thickness ##d\theta##
##dm = \frac{M}{4/3 \pi R^3}*\pi R^2\cos^2\theta* Rd\theta##
Therefore ##dI = r^2 dm = R^2\cos^2\theta dm## r is the distance from the axis to the disc which is same as ## R\cos\theta##
Then I do the integration ##I = \int_\frac{-\pi}{2}^\frac{\pi}{2} dI##
As I am getting a ##\cos^4\theta## I am not able to get the answer ##2/5 MR^2##
Can someone tell me if I have gone wrong anywhere in what I have written above?