Laurie K
- 85
- 38
This post is about the methodology required to produce the Fig. 9 Part C “optical appearance” plot as calculated by Øyvind Grøn in "Space geometry in rotating reference frames: A historical appraisal". http://areeweb.polito.it/ricerca/relgrav/solciclos/gron_d.pdf
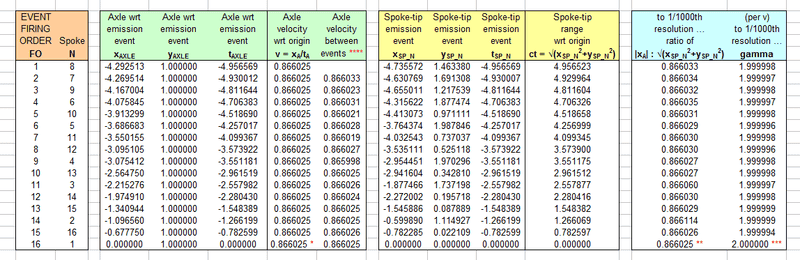
In 2014 I contributed to a thread (on another forum, pm me for the details) that verified how the Fig. 9 Part C plot described above was created. This verification used t_Axle to represent the time at each event when photons would be emitted at a specific location on the circumference of the rolling ring x_SP, y_SP at t_SP where t_SP = t_Axle. The “optical appearance” chart produced in Part C is useful in that the emitted photons travel in a straight line from their emission point to the observer and can be measured as such. Also any point on the circumference of the ring can be regarded as a point on the tip of a wheel spoke that can be length contracted to identify the correct emission point at relativistic velocities. Section 7 of Grøn's conclusion refers to this transformation.
Grøn didn't really give much away on how he created his Part C plot so it's interesting to note that the plot shown below satisfies the rules given below even if the results are slightly different. The methodology to the solution is very simple as the oval shape shown in Grøn's Fig. 9 Part C is just the valid solutions for |t_Axle| - Sqrt[x_SP^2+y_SP^2] = 0. i.e. where the time the axle takes to get from the emission time to the camera point equals the length of a straight line from the emission point to the point where the camera is i.e. the photons direct paths to point 1.
In the image below the ring is rolling from left to right at 0.866025c
the Peak Value x, y, t is -3.464, 2, -4
which is also a valid solution for |t_Axle| - Sqrt[x_SP^2+y_SP^2] = 0.
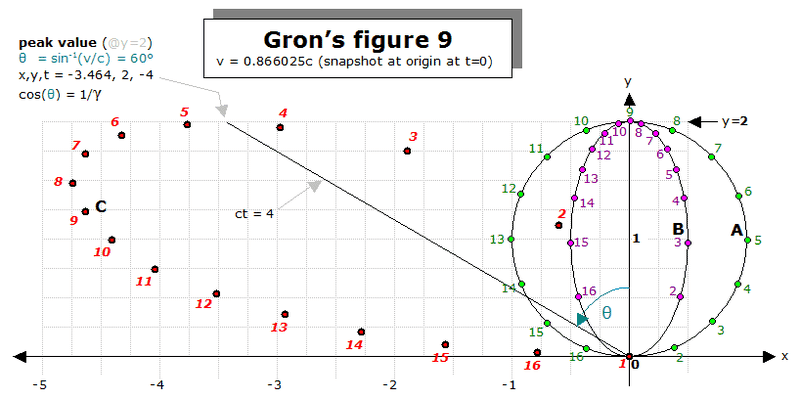
Even the axle velocity between the emission events remains constant throughout.
Has anybody solved this problem in a different manner?
The positions of points on a rolling ring at retarded points of time were calculated with reference to K0 by Ø. Grøn [111]. The result is shown in Fig. 9. Part C of the figure shows the “optical appearance” of a rolling ring, i.e. the positions of emission events where the emitted light from all the points arrives at a fixed point of time at the point of contact of the ring with the ground. In other words it is the position of the points when they emitted light that arrives at a camera on the ground just as the ring passes the camera.
In 2014 I contributed to a thread (on another forum, pm me for the details) that verified how the Fig. 9 Part C plot described above was created. This verification used t_Axle to represent the time at each event when photons would be emitted at a specific location on the circumference of the rolling ring x_SP, y_SP at t_SP where t_SP = t_Axle. The “optical appearance” chart produced in Part C is useful in that the emitted photons travel in a straight line from their emission point to the observer and can be measured as such. Also any point on the circumference of the ring can be regarded as a point on the tip of a wheel spoke that can be length contracted to identify the correct emission point at relativistic velocities. Section 7 of Grøn's conclusion refers to this transformation.
7. One may introduce local coordinates in the neighbourhood of arbitrary points on a rotating disk by means of differential transformations from coordinates in the inertial rest frame of the axis. These transformations may be chosen so that the spatial line element at constant time in the rotating system has Euclidean form. Also one may calculate a non-vanishing Riemann curvature tensor for spacetime in the rotating frame by employing the usual formulae valid in a coordinate basis. This does not mean, however, that the 3-space is flat and spacetime is curved in the rotating frame. Taking account of the non-vanishing structure coefficients in a non-coordinate basis one finds that the 3-space is curved and spacetime is flat in the rotating frame.
Grøn didn't really give much away on how he created his Part C plot so it's interesting to note that the plot shown below satisfies the rules given below even if the results are slightly different. The methodology to the solution is very simple as the oval shape shown in Grøn's Fig. 9 Part C is just the valid solutions for |t_Axle| - Sqrt[x_SP^2+y_SP^2] = 0. i.e. where the time the axle takes to get from the emission time to the camera point equals the length of a straight line from the emission point to the point where the camera is i.e. the photons direct paths to point 1.
In the image below the ring is rolling from left to right at 0.866025c
the Peak Value x, y, t is -3.464, 2, -4
which is also a valid solution for |t_Axle| - Sqrt[x_SP^2+y_SP^2] = 0.
Even the axle velocity between the emission events remains constant throughout.
Has anybody solved this problem in a different manner?