Calculating the Period of Oscillations of a Homogenous Disc

[stunner5000pt]

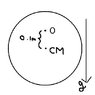
A homogenous disc of radius r = 0.20m can oscillate as a physical pendulum around a horizontal acxis O located 0.10 m from teh center of the mass of the disc. The disc is perpendicular to O. Find the period of oscillations of the disc. And graivity is 9.8 m/s^2

Is this anything like a torisonal pendulum??

Parallel axis theorem would say that the moment of inertia of the disc would be I = \frac{1}{3} MR^2 + M (\frac{R}{2})^2 = \frac{7}{12} MR^2 this is the inertia of the disc about this point O.

but what about the torque = I alpha = I (second deriavtive of angular displacement with respect to time)

please help...

 

[jamesrc]

First thing: double-check your expression for the moment of inertia of a disk.

Your use of the parallel axis theorem is fine.

You should use torque = I alpha. What are the torques on the body? (there's only one; write an expression for it.) You'll need to make an assumption about small oscillations to finish up. Your equation of motion will look like A\ddot{\theta} + B\theta = 0. You should know how to find the natural frequency of an equation that looks like that, which can be used to solve for the period of oscillation. Let us know if you need more help.

 

[stunner5000pt]

im not quite sure if the moment of inertia expression is corerct because 1/3 MR^2 is only for a disc about an axis through the center perndicular to the disc
I mnot sure how the parallel acis theorem is fine ... i think
I = \frac{1}{4} MR^2 + M (\frac{R}{2})^2 = \frac{1}{2} MR^2


isnt the other torque gravity??

I.e. mg sin \theta \frac{R}{2} ?? Because the arm is half the radius of the disc?

what kind of assumption... That at an angle of 0 the t = 0 ??

am i totally off?? I am sorry i m not good with pendulums..

 

[jamesrc]

The moment of inertia for a homogeneous disk (about the center) is 1/2 MR^2, not 1/3

so to find the moment of inertia about the pivot point:

I = I_o + MH^2 = \frac{1}{2}MR^2 + M\left(\frac{R}{2}\right)^2 = \frac{3}{4}MR^2

unless I've made a mistake...

The other torque is from gravity and your expression is correct for its magnitude.

Now you have to write the equation of motion.

As far as the assumption you have to make: what is \sin\theta approximately equal to when θ is small?