Calculating the Volume of a Tetrahedron using Integration Method

[paraboloid]

Volume of Tetrahedron[Solved]

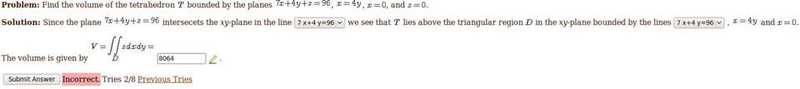
My textbook opts to integrate with respect to y before x(dydx vs dxdy), so I assumed that it would not affect the outcome.

I set the upper and lower bounds of y, respectively, as y = 24 - 7x/4 (from 7x+4y=96) to y = x/4 (from x = 4y). For x I set it from upper bound x = 12 (using x/4 = 24 - 7x/4) to lower bound x = 0 (given).

Integrating with respect to y, I get $$\int(96y - 7xy - 2y^2)|dx$$ which after inputing the bounds become $$\int(1152-144x+8x^2)dx$$. After integrating this I get $$(1152x - 72x^2 + 8x^3/3)|$$.
Computing this I get 1152(12) - 72(144) + 8(1728)/3 = 13824-10368+4608 = 8064.

I've been at this for a few hours now, but I can't seem to find my error.
Any help would be great,
Thanks in advance

 

[LCKurtz]

It would be good to learn a little tex to make it easier to read. Just click on the equation to see it:

$$\int_0^{12}\int_{\frac x 4}^{24 - \frac {7x}{4} }dydx$$

If I read your post correctly, this is how you set up the integral and it is correct. You just need to chase down the arithmetic error in your calculation, which, unfortunately, I don't have time right now to help you with. Good luck.

 

[rs1n]

I get 8x^2 - 192x + 1152 after integrating w/ respect to y.

 

[paraboloid]

Thank you both! I'll definitely work on my latex once things settle down so that I don't cause so much confusion. And yes, in fact I add 24 to -168 instead of subtracting.