Calculating Time to Reach Ground from Rocket Launch

[Joakim 1]

Homework Statement

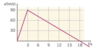
How much time does it take from the rocket gets shot up, till it reaches the ground again?
The rocket accelerates 30m/s^2 for the first 3 seconds, and accelerates downwards -6m/s^2 after.

Homework Equations

(v-v0) / a = t to find time

The Attempt at a Solution

2ad=v^2-v0^2

d= time
v=speed before landing
v0= starting speed 45m/s

I found v0 to be 45, (810/18)
810m the highest it gets, after 18 seconds.

i find v0^2 to be 2025

the distance must be 810 times 2? so 1620meter

I know the acceleration is -6 but ill just write 6 here for now
2*(6)*1620= 19440

2025+19440=21465

so v^2=21465

v=146

i go back to v=v0+at

(v-v0) / a = t

(146 - 45) / 6 = 16

the answer is supposed to be 34sec, and I am confused:)
my guess is i do something wrong with v or v0, i take v0 as the starting point (at 18 sec)

 

[kuruman]

You have found correctly that it takes 18 s for the rocket to reach a maximum height of 810 m. What is the instantaneous speed of the rocket at this max. height? Given this initial speed, how long will it take for it to come back down? Add this to the 18 s.

 

[jambaugh]

You will need to break the problem into two segments since the rocket has different stages of acceleration and you're quoting formulas which assume constant acceleration.

Question 1: Where is the rocket and how fast is it moving after the first 3 seconds of upward acceleration, given it starts at rest on the ground.
Answer 1: x = Bla, v = Bla-Bla

Question 2: How long does it take a rocket with initial position x=Bla and v = Bla-Bla to stop ascending and fall back down to a height of x=0?
Answer 2: t = Bla-Bla-Bla

Final answer to the whole question: 3s + Bla-Bla-Bla since we include both times together.

In both stages of the relevant equations will be:
$(v-v_0) = a(t-t_0)$ and $(x-x_0) = v_0(t-t_0) + \frac{1}{2}a(t-t_0)^2$, where $x$ is the position and $v$ the velocity at time $t$ and where $x_0, v_0$ is the position and velocity at #t_0# and #a# is the constant acceleration. Pick $x=0$ as the ground and fire away.

 

[Joakim 1]

You have found correctly that it takes 18 s for the rocket to reach a maximum height of 810 m. What is the instantaneous speed of the rocket at this max. height? Given this initial speed, how long will it take for it to come back down? Add this to the 18 s.

The speed is 0, i figured after reading your comment
im not sure what i do wrong, when v0=0

2ad=v^2-v0^2
2*6*810=v^2-v0^2

im only getting v to be 98..and when i do
(v-v0) / a = t (right?)
i end up with 98/6 which is wrong..

 

[kuruman]

2ad=v^2-v0^2
2*6*810=v^2-v0^2

You are using the wrong equation for the job. You need an equation that involves time and distance. Solve this problem: A rocket starts from rest at 810 m and drops down with an acceleration of 6 m/s². How long does it take to hit the ground?

 

[Joakim 1]

You are using the wrong equation for the job. You need an equation that involves time and distance. Solve this problem: A rocket starts from rest at 810 m and drops down with an acceleration of 6 m/s². How long does it take to hit the ground?

2ad=v^2-v0^2
2*6*810=v^2-v0^2

v^2=9720
v=98

v=v0+at
t=(v-v0)/a
t= 98/6 = 16sec

16 +18=34sec

is this wrong?

 

[haruspex]

16 +18=34sec

is this wrong?

Looks about right, but could be more accurate.
As @jambaugh noted, there is a better way to subdivide the problem. For the purposes of the question, there is nothing special about reaching maximum height; what is special is the change in acceleration.

So we have first stage
a=30m/s²
t=3s
v_i=0
v_f=90m/s
s=v_it+½at²

Second stage
a=-6m/s²
s=-s from first stage
v_i=v_f from first stage.
s=v_it+½at²

Solve to find t, being careful to select the correct root.