jocose
- 12
- 1
1. The problem statement, all variables, and given/known data

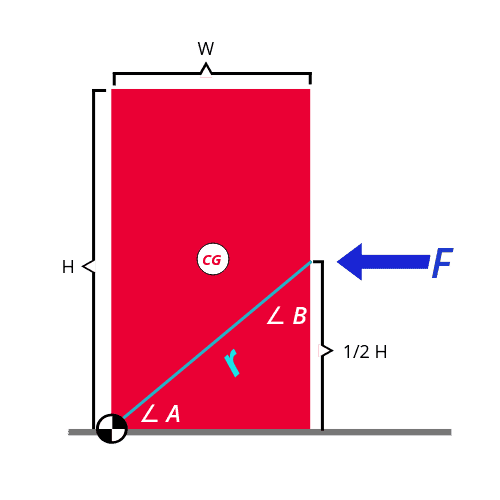
If I apply a force perpendicular to the side of a 2D block at 1/2 its height with a fixed bottom corner opposite the applied force how much force will be required to tip the block?:
[/B]
If I understand correctly the torque of the applied force will equal F⋅ r ⋅ cos( ∠A ). The cos( ∠A ) is used because the force is being applied perpendicular to the side of the block, not the axis it's rotating in. This will reduce the torque by cos( ∠A ).
What I don't understand is how to calculate the opposing force to see if the resulting torque of the applied force is enough to overpower it.
Specifically, I am confused by the fact that the force is being applied half way, and not at the top of the block. How should the weight above the applied force be quantified?
(NOTE: I am not an enrolled student nor do I have any formal training, I am trying to teach myself. I am making an effort to read texts but it's become overwhelming and I'm looking for some guidance )

If I apply a force perpendicular to the side of a 2D block at 1/2 its height with a fixed bottom corner opposite the applied force how much force will be required to tip the block?:
- Block Mass = M
- Block Width = W
- Block Height = H
- Applied Force = F
- Distance between force and pivot = r
Homework Equations
The Attempt at a Solution
[/B]
If I understand correctly the torque of the applied force will equal F⋅ r ⋅ cos( ∠A ). The cos( ∠A ) is used because the force is being applied perpendicular to the side of the block, not the axis it's rotating in. This will reduce the torque by cos( ∠A ).
What I don't understand is how to calculate the opposing force to see if the resulting torque of the applied force is enough to overpower it.
Specifically, I am confused by the fact that the force is being applied half way, and not at the top of the block. How should the weight above the applied force be quantified?
(NOTE: I am not an enrolled student nor do I have any formal training, I am trying to teach myself. I am making an effort to read texts but it's become overwhelming and I'm looking for some guidance )
Last edited: