Calculating Total Moment of Force F1 about Point A

  • Thread starter Thread starter United
  • Start date Start date
  • Tags Tags
    Moment Value
AI Thread Summary
To calculate the total moment of force F1 about point A, the formula used is moment = perpendicular distance x force. The user determined the resultant distance as sqrt(20) and attempted to apply trigonometric functions for angles 35 and 55 degrees but encountered difficulties. The correct approach involves identifying the angle θ between the line connecting point A to the force application point and the force's line of action. To find θ, one must drop perpendiculars from point B to both the force line and a line through A parallel to the force. This method will help in accurately calculating the moment.
United
Messages
7
Reaction score
0

Homework Statement


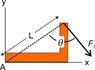
http://i.imgur.com/Laub8lL.png
Find the total moment created by force F1 about point A.

Homework Equations


moment = perpendicular distance x force


The Attempt at a Solution


I got my resultant distance to be squrt(20). With this in mind, I plugged into my calculator:
sqrt(20) x 12 x (insert values listed below)
(numbers in degrees)
cos(35)
sin(35)
cos(55)
sin(55)

and I've had no luck with any of this.

Please help me
 
Physics news on Phys.org
The moment is
FL sin(θ)
where θ is the angle between the line connecting point A and the point where F acts on the structure and the line of action of the force
 
How do i find theta though?
 
See drawing
 

Attachments

  • moment.jpg
    moment.jpg
    18.6 KB · Views: 425
Call the point where the right-angled bend is B.
Drop a perpendicular from B to the line of the force. What's the length of it?
Drop another from B to a line through A parallel to the force. What's the length of that?
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Minimum force to tip the bin over
Replies
7
Views
922
Understanding The Concept Of Moments
Replies
6
Views
2K
To find the angle between the ground and rods in limiting friction
Replies
5
Views
2K
How is the moment at A using the Force 1200N calculated?
Replies
22
Views
2K
To find direction and magnitude of forces acting in a system
Replies
2
Views
1K
Force on 2 cables with weight attatched using Theta....
Replies
3
Views
2K
Calculating Forces in a Leg: Gait Analysis and Joint Reaction Force
Replies
7
Views
1K
Equilibrium of Rigid Bodies. Rafter. What is moment arm?
Replies
1
Views
3K
How do you calculate the moment of a force about a point?
Replies
1
Views
1K
What's the Total Force Exerted on the Skater?
Replies
4
Views
1K

Hot Threads

Recent Insights

Back
Top