postfan
- 259
- 0
Homework Statement
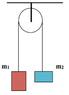
Two masses, m1 and m2, are hung over a pulley as shown. Assume that m1 is heavier, that the pulley is massless and frictionless, and that the rope does not slip. The blocks are held motionless and then released. Determine the magnitude of the velocity of m1 after it has fallen a distance of d meters. You may enter "m_1" for m1 and "m_2" for m2.
Homework Equations
The Attempt at a Solution
Found the acceleration of the 2 objects, (m_1+m_2)*g, but got stuck after that.