alexialight
- 7
- 0
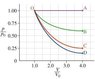
Calculate the work W done by the gas during the isothermal expansion (path C). It may be be convenient to generalize your results by using the variable R_v, which is the ratio of final to initial volumes (equal to 4 for the expansions shown in the figure.)
Express W in terms of p_0, V_0, and R_v.
I've been at this question for ages and I just can't see how p_0 fits into the answer. The hints say to find an expression for p(V) in terms of p_0, V_0 and V and I can't even seem to do that. Any help would be much appreciated.
Express W in terms of p_0, V_0, and R_v.
I've been at this question for ages and I just can't see how p_0 fits into the answer. The hints say to find an expression for p(V) in terms of p_0, V_0 and V and I can't even seem to do that. Any help would be much appreciated.