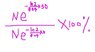Calculation Error: Iodine-131 Half-Life & 30 Days

[Ukitake Jyuushirou]

Iodine-131 is used in treatment of thyroid disorder. This isotope has a half life of 8.04 days, what percentage of an initial sample is left after 30 days?

having done, the initial calculations by taking 30 divided by 8.04 to find how many hl will have passed i take the number and i take the mass number divided by the amount of hl that has passed times 100 but my answers dun match the answer in the book.

where did i go wrong?

 

[Barkeeper Moe]

No of HLs = 3.7313432835820895522388059701493

No of HLs   Activity	%
0	    131		100
1           65.5	50	
2           32.75	25
3           16.375	12.5
4           8.1875	6.25

So its somewhere between 12.5% and 6.25%... Cant quite remember how to do it exactly.

My guess would be from 3 > 4 the loss is 8.1875
So from 3 > 3.7313432835820895522388059701493 the lost would be 8.1875 * 0.7313432835820895522388059701493 = 5.9878731343283582089552238805949
So then take that away from the activity @ 3 HLs = 16.375 - 5.9878731343283582089552238805949 = 10.387126865671641791044776119406
The work out the percentage, so 10.387126865671641791044776119406 / 131 * 100 = 7.9291044776119402985074626865695 = 7.93% (2dp)

 

[HallsofIvy]

"Taking the number" is not a mathematical operation! You don't need to do anything with the "mass number" since you are only asked about percentage of the original amount, not "what mass was left".
Take the orginal amount to be 100%, multiply that by
(\frac{1}{2})^{\frac{30}{8.04}}

 

[Ukitake Jyuushirou]

thanks to all who helped, upon thinking back and reviewing the formulas for this chapter i found the answer. here is the solution for anyone who cared...