Jony S
- 14
- 0
Homework Statement
[/B]
Hello, I would like to request some help in solving this mechanics problem.
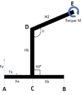
Consider the attached drawing of a solid structure which is pinned to the ground on points A and B.
Distances AC=Xa, CB=Xb, CD=H1 and DE=H2
A torque with magnitude M is applied on point E. How do I determine the resulting forces from this torque Fx and Fy on point A and point B ?
Homework Equations
This would be the equation for torque M
M=r*F
The Attempt at a Solution
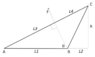
My guess is that we can bypass the "middle" geometry of the structure, and simply use the distance from point A to point E (let's call it RAE), and its angle with the horizontal (θAE).
The resulting force would thus be F = M/RAE, with Fx = Fcos(θAE) and Fy = Fsin(θAE). A similar approach would be applied for point B.
Is this correct ?
Thanks in advance !

 ##\qquad## !
##\qquad## !