mastdesi
- 3
- 0
Calculus - please help find average rate of change of the function over a given interval
h(t) = sin t, [3pi/4,4pi/3]
please help me solve this, try to give me an explanation on every step please. i checked but i can't find anything on this in the book. i am basically having problem with this because of the sin.

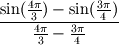
i got to there also but i don't know how to solve the sin part. how does the square root come in.
Homework Statement
h(t) = sin t, [3pi/4,4pi/3]
please help me solve this, try to give me an explanation on every step please. i checked but i can't find anything on this in the book. i am basically having problem with this because of the sin.
Homework Equations
The Attempt at a Solution
i got to there also but i don't know how to solve the sin part. how does the square root come in.