Can a ball stay on a track with a given height and friction coefficient?

[yoni162]

Homework Statement

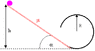
A ball is released from height h. The friction coefficient between the straight part and the ball is 'u'. I need to find the smallest h so that the ball doesn't fall off the track.
The angle alpha=45 degrees.

Homework Equations

Work of non-conservative forces = Change in mechanical energy

The Attempt at a Solution

I calculated the work done by the friction force while the ball is going down the straight part.
Wf=-u*mg*cos(alpha)*X

X=the length of the straight part.

We get that:
Wf=-u*mg*h

since cos(alpha)/sin(alpha)=1

Now I want to say that Wf=change in mechanical energy, so:

-u*mg*h=mg(0-h)+0.5*m(v^2-0)

when v=the velocity of the ball when it reaches the end of the straight part. We get:

v^2=g*h(1-u)

Now to the second part, the frictionless rail. Since all the forces are conservative now:

0.5*m*V1^2=0.5*m*V2^2+mg2R

When V1^2=g*h(1-u) -----> (the velocity we found before)
V2=the velocity at the top of the loop

So I want that V2>0, so after some work we get:

h>(2R)/(1-u)

but when I put in a numerical answer I'm told that I'm wrong. Is there a mistake in my solution?

 

[nasu]

The condition v>0 at the top is not sufficient for the ball to stay on the track.
You need to have the reaction force acting on the ball at the top to be >=0.

 

[yoni162]

The condition v>0 at the top is not sufficient for the ball to stay on the track.
You need to have the reaction force acting on the ball at the top to be >=0.

yeah you're right I forgot, thanks..