Okazaki
- 56
- 0
Homework Statement
(This is a continuation of the problem where I proved Torricelli's Law: v = √(2gh))
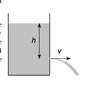
The water level in a tank lies a distance H above the floor. There is a hole in the tank that a distance h below the water level
a.) Find the distance x from the wall of the tank at which the leaked stream of water hits the floor
b.) Could another hole be punched at another depth h' so that this second stream would have the same range? If so, at what depth?
Homework Equations
Δx = (vf2 - vi2)/g
v = √(2gh)
The Attempt at a Solution
At first, I was not really sure what to do here at all (and I probably ended up solving it completely wrong.)
So, basically, I wasn't exactly sure how to find the distance, since I only knew the initial velocity in the x direction (or, at least, I assumed v = √(2gh)) was the velocity of the water in the x direction based off the picture in the problem.)
So, what I tried was:
(Since the equation I had to derive from Torricelli's law in the problem I had to do before this ended up being Δv = √(2gh), I assumed:)
Δx = (2gh)/g
= 2h
For b, I'm completely confused on even where to begin solving for the equation.