How to find the velocity of a water leak in a spinning tank

[DigitalCrush]

Homework Statement

Spinning water tank with a leak and constant angular speed

Relevant Equations

Bernoulli equation, constant acceleration kinematic equations, uniform circular motion equations.

We have a cylindrical water tank that spins over its axis of symmetry with constant angular velocity ω. Here's a diagram:

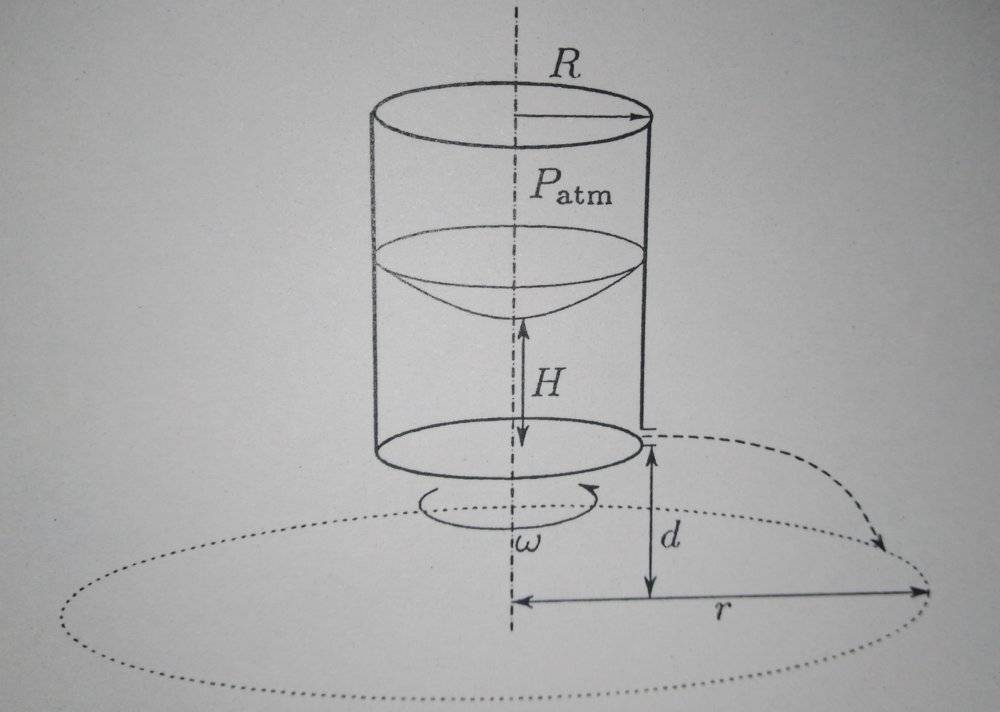
We wish to find:
1 - The tangential and radial components of the velocity of the water as it leaves the tank.
2 - The radius r reached by the water.

I'm not sure at all about how to handle the fact that the tank spins, as well as the deformation in the water surface. I chose to apply Bernoulli's equation and compare the point at the center of the surface, and the point where water leaves the tank:

$P_{atm} + \delta g_{ef} H = P_{atm} + \frac{1}{2} \delta v_{r}^2$. So: $v_{r} = \sqrt{2Hg_{ef}}$

Where $g_{ef} = g + a_{c} = g + R\omega ^2$ is the effective acceleration of the water.

Then we have: $v_{r} = \sqrt{2H(g + R \omega ^2)}$

The tangential component of the water's velocity is: $v_{t} = R \omega$

The time it takes the water to reach the floor is $t = \sqrt{\frac{2d}{g}}$, and $r = R + v_{r}t$.

Thus: $r = 2\sqrt{Hd(1 + \frac{R \omega ^2}{g})} + R$

My issue is that I have no idea if my $g_{ef}$ is correct. It seems to make sense because I expect $r$ and $v_{r}$ to be higher the larger $ω$ is. But I don't know how to explain why it makes sense to use it. That is, if it's even correct to begin with. I'm also not sure about using $a_{c}=Rω^2$ because I'm using the center point of the water surface, which is at $r=0$.

Any help is appreciated. Thanks.

 

[haruspex]

not sure at all about how to handle the fact that the tank spins

I couldn't follow your reasoning.
Suppose the difference in the height of the top surface between the centre and the edge is Y. I considered that:
- the pressure is constant across the exposed parabolic surface
- the surface profile is independent of the depth of liquid, so if we consider a surface within the drum the same as at the top surface (i.e., the top surface profle but replicated at some depth) the pressure will be constant across that.
- if we imagine the drum extended downwards, we can choose such a parabolic surface such that at the edge it touches the hole. The depth at its centre would be H+Y.
Is it reasonable to say that the pressure at that H+Y depth is ρg(H+Y)?
If so, that gives us the pressure at the hole.

 

[DigitalCrush]

I think I understand most of your reasoning, but I'm not sure about how I could obtain Y in terms of the given data. Also, wouldn't the pressure at the hole be Patm, since it's exposed to the exterior of the tank?

Without obtaining Y in terms of the other quantities and assuming the pressure at the hole is $\delta g (H+Y)$, I tried to get $v_{r}$. By comparing the point at the center of the surface of the water and the hole (with height $0$ at the hole), I got:

$\delta g (H+Y) + \frac{1}{2} \delta v_{r}^2 = P_{atm} + \delta g H$

So $v_{r} = \sqrt{\frac{2P_{atm}}{\delta} - 2gY}$

I'm not sure about this because I expect $v_{r}$ to be higher as $\omega$ increases, and I would expect $Y$ to also get larger as $\omega$ increases. By this formula, $v_{r}$ would actually be smaller as the tank spins faster.

 

[haruspex]

wouldn't the pressure at the hole be Patm, since it's exposed to the exterior of the tank?

The pressure just outside the hole is one atmosphere. To find the radial velocity of the jet you need the pressure difference from just inside. Compare with the equation with no rotation.

obtain Y in terms of the given data

I assumed you wouid know how to compute the surface of a rotating fluid.
Consider a small parcel of water on the surface at some radius x. Find an equation relating its tangential velocity to the slope of the surface and solve the differential equation.

 

[jbriggs444]

Find an equation relating its tangential velocity to the slope of the surface and solve the differential equation.

Equivalently, consider the centrifugal force field. Integrate from x=0 to x=R to get the associated potential (the centrifugal pressure field). Add this to the pressure at the center of the bottom.

 

[haruspex]

Equivalently, consider the centrifugal force field. Integrate from x=0 to x=R to get the associated potential (the centrifugal pressure field). Add this to the pressure at the center of the bottom.

Yes, that looks simpler.

 

[DigitalCrush]

I found that $Y = \frac{1}{2} \frac{\omega ^2}{g} R^2$. If the pressure at the hole is $\delta g (H+Y)$, then using Bernoulli's equation in the hole and the center of the water surface gives me: $\delta g (H+Y) + \frac{1}{2} \delta v_{r}^2 = P_{atm} + \delta g H$.

So $v_{r} = \sqrt{\frac{2P_{atm}}{\delta} - 2gY} = \sqrt{\frac{2P_{atm}}{\delta} - \omega^2 R^2}$.

I expected that a larger $\omega$ would mean a larger $v_{r}$. Is this right?

 

[haruspex]

I found that $Y = \frac{1}{2} \frac{\omega ^2}{g} R^2$. If the pressure at the hole is $\delta g (H+Y)$, then using Bernoulli's equation in the hole and the center of the water surface gives me: $\delta g (H+Y) + \frac{1}{2} \delta v_{r}^2 = P_{atm} + \delta g H$.

So $v_{r} = \sqrt{\frac{2P_{atm}}{\delta} - 2gY} = \sqrt{\frac{2P_{atm}}{\delta} - \omega^2 R^2}$.

I expected that a larger $\omega$ would mean a larger $v_{r}$. Is this right?

A few things wrong there.
Atmospheric pressure applies both at the top of the liquid and just outside the hole, so cancels.
The excess pressure just inside the hole is is $\delta g (H+Y)$, but I do not understand how you obtained your "Bernoulli’s equation". You should take the radial velocity as zero just inside the hole and v_r just outside.