Can a truss with released ends still form a mechanism?

Click For Summary

Discussion Overview

The discussion revolves around the modeling of a truss structure with released ends and the conditions under which it may form a mechanism. Participants explore the implications of releasing joints and the stability of the truss, particularly focusing on the role of a central node and the geometric configuration of the truss.

Discussion Character

  • Technical explanation
  • Debate/contested

Main Points Raised

  • One participant describes a truss model where all joints are released except for one, yet a mechanism still appears to form, leading to confusion about the stability of the structure.
  • Another participant suggests that the absence of a center node leads to instability, arguing that the triangles necessary for stability do not exist without it.
  • A different viewpoint proposes that removing certain bars can lead to mechanisms forming, specifically mentioning the configuration of bars that can be deleted to create a "crossed quadrilateral" or "bowtie" structure.
  • Some participants assert that the structure is statically indeterminate and cannot be analyzed using standard methods for statically determinate structures, emphasizing the complexity introduced by the lack of a center node.
  • There is a correction regarding the stability of the structure without a center node, with one participant acknowledging the previous error in their understanding.

Areas of Agreement / Disagreement

Participants express disagreement regarding the stability and mechanisms of the truss structure. Some argue that the absence of a center node leads to instability, while others contend that the structure can still be stable and statically indeterminate. The discussion remains unresolved with competing views on the implications of the truss configuration.

Contextual Notes

The discussion highlights limitations in the analysis of the truss due to its statically indeterminate nature and the absence of a central node, which complicates the application of standard analytical methods.

gabuchia
Messages
2
Reaction score
0
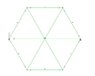
Dear all! I have encountered a problem with modelling a truss.

When modelling on an analysis software, you must release the ends of the joints, but not all
or it will form a mechanism, therefore you release all but one of the joint.
But what I have here, is a truss that is released on all ends except for one for every joint,
yet a mechanism still seems to occur here are the pictures! They're attached!
Try modelling it! If it is possible, please do let me know what the problem is! This little experiment is driving me nuts =D. All I could pull out is that, one of the nodes will rotate, but I can't make sense out of it.

Thanks!

Edit: the centre is not a node
 

Attachments

  • Truss1.JPG
    Truss1.JPG
    12.7 KB · Views: 672
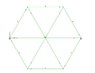
  • Truss2.JPG
    Truss2.JPG
    12.1 KB · Views: 605
Engineering news on Phys.org
If the center is not a node, you have instability, since your triangles don't exist. Pin everything together at the center node.
 
To see what the mechanism is with one diagonal removed, suppose you remove the horizontal one.

Then, bars 2 and 5 form a mechanism so you can delete them, and the same for bars 4 and 7.

The 4 bars that are left form a "crossed quadrilateral" or "bowtie" which also has a mechanism.

Post #2 is wrong. The complete structure doesn't have any mechanisms without a center node, even though it can't be decomposed into triangles. But it is not statically determiate, so you can't analyse it with the "standard" methods for statically determinate structures. The forces in the different bars depend on their relative stiffness as well as on the applied loads.

The main reason why people used to design trusses from triangles only was so they WERE statically determinate and easy to analyse by hand, not because they were the most efficient structural designs.
 
AlephZero said:
Post #2 is wrong. The complete structure doesn't have any mechanisms without a center node, even though it can't be decomposed into triangles. But it is not statically determiate, so you can't analyse it with the "standard" methods for statically determinate structures.

Indeed, the structure is statically indeterminate, yet stable without the center node. Sorry about that, thanks for the correction.
 

Similar threads

Truss behaviour, load-deformation curve
  • · Replies 3 ·
Replies
3
Views
2K
How to check the Stability of ANY Truss?
  • · Replies 1 ·
Replies
1
Views
2K
Understanding Truss Analysis: Investigating the Accuracy of a Bridge Design App
  • · Replies 3 ·
Replies
3
Views
3K
Forces in a Howe truss (2D) pinned at BOTH ends
  • · Replies 18 ·
Replies
18
Views
7K
Method of Joints Query: Shedding Light On Truss Calculations
  • · Replies 1 ·
Replies
1
Views
2K
Why does ENGR Mechanics: Statics cover *hinged* trusses?
  • · Replies 2 ·
Replies
2
Views
1K
How Can a Turnbuckle Mechanism Release Upon Impact?
  • · Replies 22 ·
Replies
22
Views
2K
Efficient way to solve truss by hand
  • · Replies 7 ·
Replies
7
Views
4K
How Do X-Braces Affect Indeterminate Truss Analysis?
  • · Replies 2 ·
Replies
2
Views
3K
Star maps using Blender
  • · Replies 19 ·
Replies
19
Views
2K