Buckling and modal FEA of a submarine structure

[Vigardo]

TL;DR Summary

How should floating or underwater structures like submarines, capsules or buoys be modeled by FEA to obtain feasible buckling and normal modes? Thanks!

Dear FEA experts,

I'm trying to model the mechanical behavior (static, modal, and buckling analyses) of an underwater floating structure (e.g. submarine capsule or buoy) under hydrostatic pressure by Finite Element Analysis.

To obtain feasible results, the structure should be modeled as freely suspended, i.e. attached to nothing or with no-supports, am I right? However, most software available requires supports to perform calculations.

How should I perform FEA to get feasible results with a floating structure?

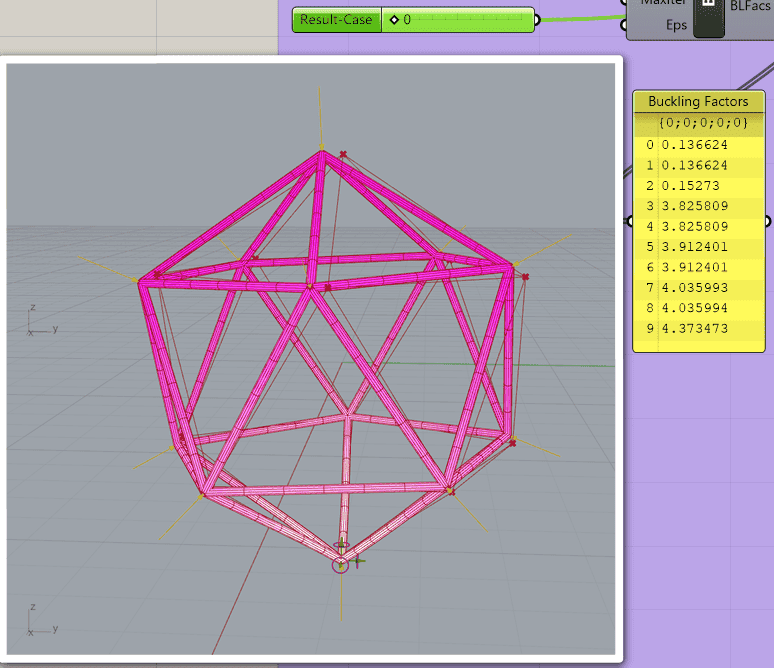
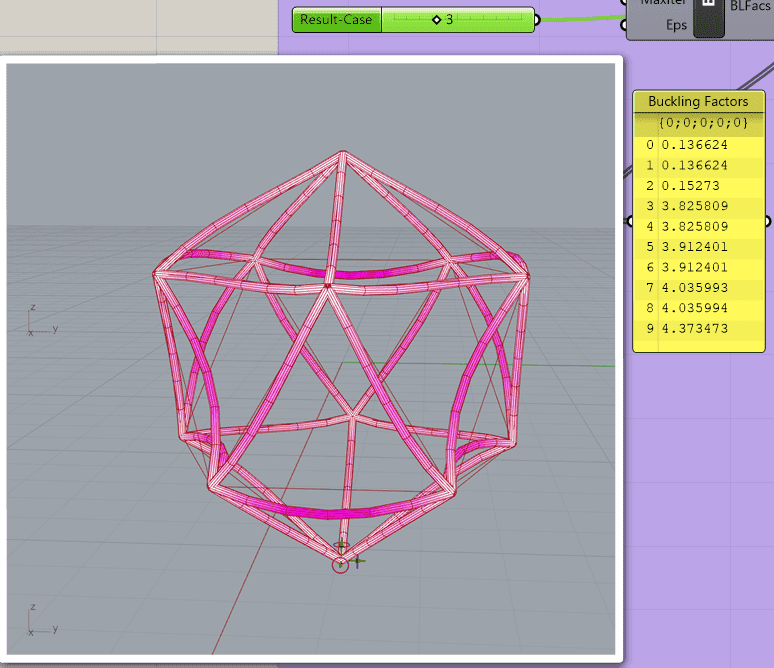
If I fix the 6 DoFs of one vertex, it is possible to obtain a feasible static analysis. Unfortunately, this unrealistic constraint severely affects both the buckling and the normal modes. The first three frequencies as well as the first three buckling factors are too low, as you can check in the two following images obtained in Karamba3D (parametric engineering software). In the images, the first 10 buckling factors and the differences between the 1st (unfeasible) and the 4th (feasible) buckling modes are shown for an icosahedral capsule:

I've found a web about Free-Floating FEA models where the author explains the 3-2-1 method. This method seems to work for the static analysis of floating (unsupported) structures. In this forum thread, “jhardy1” user says two relevant things:

1. If your structure is “free-floating” (e.g. aircraft in flight, free vibration modes, etc), then “Inertia Relief” can be a useful technique, if your software supports it; otherwise, the 3-2-1 approach can generally be applied, but it is important to note that the restraints should be carefully positioned such as to not attract any spurious net force that can’t actually go to the fictitious support nodes.
2. In the 3-2-1 approach, you need to ensure also that the locations of the artificial restraint nodes don’t influence vibration modes shapes or buckling mode shapes of interest (e.g. if one of your restraints is halfway along a beam, you may not be able to recover the fundamental vibration mode of the beam).

Unfortunately, I'm not sure about where locate the supports of the 3-2-1 method to ensure that the artificial restraints do not influence buckling and normal mode shapes.

Please, would you help me or suggest any alternatives?

Thanks a lot in advance!

 

[jrmichler]

Use a spring support over an area, or even two areas. Then reduce the spring constant to the minimum that will keep the model from flying off into space. You may have to try different locations for the spring support(s).

 

[Vigardo]

Your solution works! Thank you very much Jrmichler!

This is the first not-close-to-zero buckling mode using one central support with all DoFs fixed and 12 very soft springs (0.1 kN/m springs for 101 kN/m2 hidrostatic pressure). Buckling factors and Normal modes frequencies are also shown.

However, there is still something that worries me: Why there are just 3 close-to-zero modes for buckling analysis whereas there are 6 for normal mode analysis? The first 3 buckling modes seem to be rigid body rotations… but what about the 3 translations? Shouldn't be there as well?

 

[jrmichler]

I have done only a few buckling analyses, and those several years ago. I was using different software, so have no idea what those near-zero modes are. My method for solving your type of problem is to go back and find out how the software handles simpler known cases. In your case, I would analyze a simple Euler column. One case with one end fixed and the other end free, another case with one fixed and the other end guided. Then compare the FEA results to hand calculations. I use FEA on real problems only after I am convinced that I know how to get correct useful answers from the FEA for those types of problems.

 

[Vigardo]

Thanks for your kind recommendations they are very helpful!

In essence, I've performed what you said but "mentally" . After deeply thinking about it I think I have some reasoning that would explain the number of close-to-zero modes differences between buckling and modal analyses. Would you check whether this is physically sound or if I'm overthinking? Sorry for the long text, it is a bit hard to explain.

Normal modes represent all the infinitesimal vibration shapes that a given system would experience without any forces, just as a consequence of its own stiffness and mass distribution. Thus, my “submarine capsule” system attached to the ground by weak springs has 6 close-to-zero vibrational modes since it should be able to almost-freely vibrate as a rigid body (3 translational + 3 rotational DoFs). So there is not problem at all here.

By contrast, the results provided by buckling analysis are different. Buckling modes represent the shapes and the critical load level that turn the system unstable. This means that above such loading level any infinitesimal displacement will not be counteracted by the corresponding reaction and the structure will fail. In other words, the reaction capacity of the system is exhausted.

For simplicity, let's consider a unidimensional (1D) case, for example, a doubly pinned column axially compressed. When compression force reaches the critical Euler buckling load, the capacity of the column to withstand infinitesimal lateral perturbations disappears (i.e. the external load action in the infinitesimally distorted column produces a greater torque than the reaction the column is able to produce) and thus buckles according to the well known “compressed spaghetti” shape.

If the support and its reaction force are replaced by an external load (equal but opposite to the load on top) and two dummy weak springs at both ends attached to fixed supports, the system becomes analogue to my floating capsule problem (practically “floating free”). In this case, the buckling mode shapes should be equivalent as for the doubly pinned case. I mean, there should not appear any translation buckling mode since this motion does not cause any instability. In other words, the reaction capacity of the dummy springs does not exhaust for any compressive load.

In the 3D case of my capsule, the 3 close-to-zero buckling modes observed are rigid body rotations because they correspond to the “rotational” buckling of the springs connecting the vertices to the central fixed node (at some loading point they do not oppose sufficiently to infinitesimal rotations). Similarly to the 1D case, there are no translation modes since any increase in compressive pressure does not reduce the capacity of the dummy springs to withstand any rigid body translation. Of course, all this reasoning depends on how springs are implemented in the FEA software.