Discussion Overview
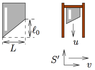
The discussion revolves around a thought experiment involving a cable car and the implications of special relativity on the simultaneity of events as perceived by different observers. Participants explore how the orientation of the cable car's fall is perceived differently by an observer on the ground and one inside the cable car, examining the effects of the relativity of simultaneity and the propagation of information through the cable.
Discussion Character
- Debate/contested
- Conceptual clarification
- Exploratory
Main Points Raised
- Some participants argue that the observer on the ground sees both cables snap simultaneously, leading to a horizontal fall of the cable car, while the observer in the car sees the front cable snap first, resulting in a downward orientation.
- Others propose that the speed at which the cable relaxes affects the timing of the fall, as the information about the break propagates at the speed of sound in the cable, which is frame-dependent.
- A few participants highlight that the orientation of the cable car is not invariant and that different reference frames can disagree about the orientation due to the relativity of simultaneity.
- Some contributions suggest that the scenario can be analogized to other systems, such as a helicopter with propellers, to illustrate the complexities of simultaneous events in different frames.
- There are discussions about whether observers can agree on the motion of a marble placed at the center of the cable car, with some asserting that they must agree on its position while others argue that the orientation cannot be agreed upon due to the effects of acceleration.
- One participant mentions that if the cable car were in free fall, the simultaneity of impacts would differ between frames, further complicating the discussion.
Areas of Agreement / Disagreement
Participants express multiple competing views regarding the simultaneity of events and the orientation of the cable car's fall. There is no consensus on how these factors interact, and the discussion remains unresolved.
Contextual Notes
Participants note that the geometry of the situation complicates the understanding of simultaneity and orientation, and that assumptions about the propagation of information and the effects of acceleration are critical to the discussion.