- #1
jaumzaum
- 434
- 33
My teacher proposed the following problem in the classroom as a challenge:
Consider 2 disks in the plane. Prove that you can always find 2 points exterior to the disks so that all the parabolas that pass through both points will intersect at least one of the disks.
I think I found a solution, can anyone check if it is right?
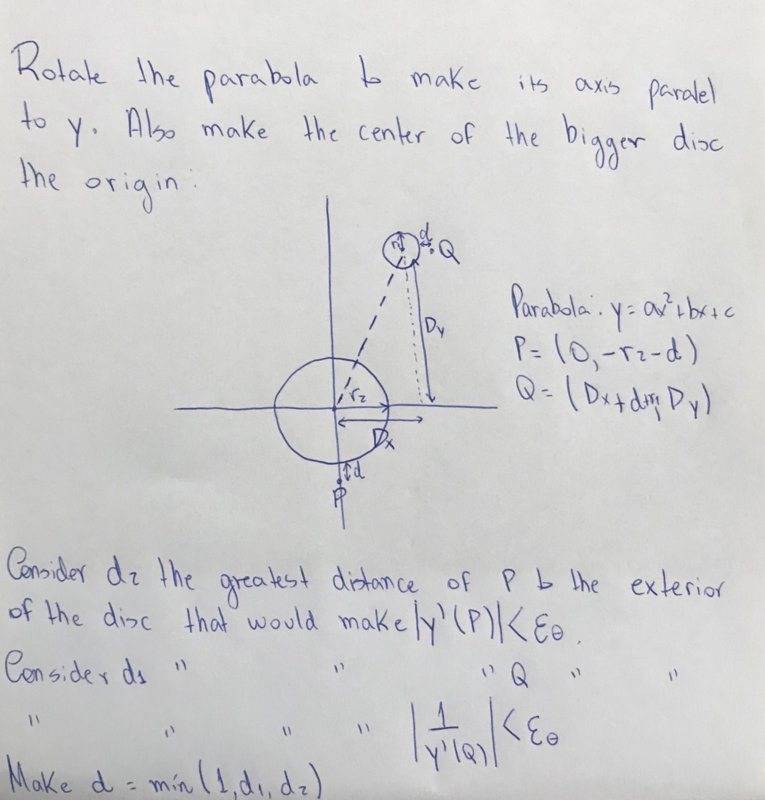

Consider 2 disks in the plane. Prove that you can always find 2 points exterior to the disks so that all the parabolas that pass through both points will intersect at least one of the disks.
I think I found a solution, can anyone check if it is right?