Can Having Enough Bends in Circuit Conductors Cause Energy Loss?

[Prince Rilian]

I am aware that when charged particles accelerate or decelerate, the particle will emit a certain amount of radiation. But since a charged particle will accelerate any time it goes around a bend in a circuit, wouldn't it radiate some energy when it goes around the bend?

I thought that giving two examples may aid in asking this question, where I can pose an "extreme case" thought experiment:

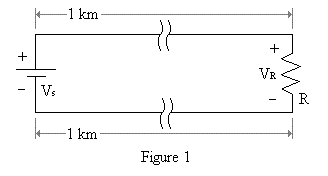
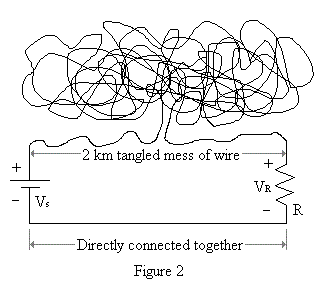
In both the above circuits, V_s is the same and the same amount of wire is used (two kilometers of it). But while the wire used Figure 1 has a minimum number of bends in it, that used in Figure 2 is a horribly tangled mess! Shouldn't the value of V_R for Figure 1 be a little higher than that of V_R for Figure 2 due to energy losses from all the bending routes the electrical current is forced to take in that circuit?

 

[UltrafastPED]

The electrons in a wire have an inherent, random motion which is orders of magnitude greater than the net drift velocity which is caused by the voltage applied.

So you can see that for a DC circuit the twists and turns will not add anything significant to the picture.

In the case of AC currents, there is no net motion for the electrons - they just move for and aft at 50 or 60 Hz, depending upon your local provider. So very few of them will see the turns at all.

There are other issues, depending upon the frequency and the current; these include radio emissions from high frequency signals, and magnetic fields. To limit the inductive coupling between wire pairs carrying high frequency data streams - they intentionally twist each pair together.

See http://en.wikipedia.org/wiki/Twisted_pair

 

[Prince Rilian]

OK. That explanation resolves the question.

Thank you!