noleknight16
- 6
- 0
A conducting rod moves with a constant velocity v in a direction perpendicular to a long, straight wire carrying a current I as shown in the figure below.
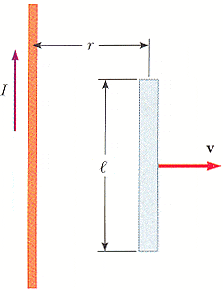
Find the EMF
It should equal U_o*V*L*I/2*pi*r, but how do I get there?
Find the EMF
It should equal U_o*V*L*I/2*pi*r, but how do I get there?
