Andy Bloch
- 4
- 0
(I hope this post doesn't cross the border into the forbidden realm of quackery and speculation.) I have what seems like a simple question about Special Relativity but I haven’t seen it discussed anywhere, nor has anyone I've asked.
Does the nonlinearity of the Lorentz factor provide a way for an asymmetric system to have momentum with zero average velocity, and vice-versa?
Consider this example:
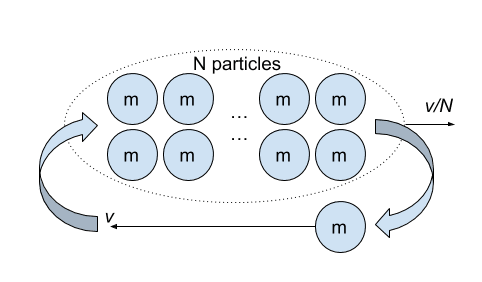
There are N + 1 identical particles in this system. At any time, there is one particle (an electron, perhaps) moving to the left with relativistic velocity v (relative to the laboratory frame), and N particles moving to the right with velocity v/N. The process can be repeated continuously. There is no net movement of the system. But, it seems that the total (relativistic) momentum is non-zero. The total momentum to the left is (assuming v/N << c):
where γ is the Lorentz factor.
Is there something I am missing?
Yes, I've ignored the periods of acceleration. But (1) if the clock hypothesis is true, making those periods very short should make any effect negligible, and (2) if the acceleration periods did affect the total momentum and exactly canceled it out, then changing the acceleration curve would have to have no effect on the total momentum. That doesn't seem likely to me.
(No, this would not seem to be a good way to power a spacecraft . It does not provide a constant thrust, just an initial velocity boost. I've done some calculations, with very generous assumptions, that suggest that even a velocity on the order of 1 m/s would not currently be feasible.)
I'm hoping someone here can quickly show me what is wrong with my math or reasoning, or provide a reference where this has been discussed.
Thanks in advance for any feedback.
Does the nonlinearity of the Lorentz factor provide a way for an asymmetric system to have momentum with zero average velocity, and vice-versa?
Consider this example:
There are N + 1 identical particles in this system. At any time, there is one particle (an electron, perhaps) moving to the left with relativistic velocity v (relative to the laboratory frame), and N particles moving to the right with velocity v/N. The process can be repeated continuously. There is no net movement of the system. But, it seems that the total (relativistic) momentum is non-zero. The total momentum to the left is (assuming v/N << c):
ptotal = γ m v - N m v / N = (γ-1) m v
where γ is the Lorentz factor.
Is there something I am missing?
Yes, I've ignored the periods of acceleration. But (1) if the clock hypothesis is true, making those periods very short should make any effect negligible, and (2) if the acceleration periods did affect the total momentum and exactly canceled it out, then changing the acceleration curve would have to have no effect on the total momentum. That doesn't seem likely to me.
(No, this would not seem to be a good way to power a spacecraft . It does not provide a constant thrust, just an initial velocity boost. I've done some calculations, with very generous assumptions, that suggest that even a velocity on the order of 1 m/s would not currently be feasible.)
I'm hoping someone here can quickly show me what is wrong with my math or reasoning, or provide a reference where this has been discussed.
Thanks in advance for any feedback.
