Momentum and energy calculation in special relativity

[liuxinhua]

TL;DR Summary

The momentum calculated by two ways is inconsistent

$\ \ \ \ \$In $K$，System $M$ is composed of a spring $N$ and four particles $P, Q, A and B$. The ends of spring $N$ are fixedly connected with particles $P and Q$ respectively. Particle $A$ is adjacent to particle $P$, and particle $B$ is adjacent to particle $Q$.
$\ \ \ \ \$Before $t_0$ , the spring is in tensile state under the action of force $F_0$ ($x$ direction)at both ends, and the spring $N$ is static, with length $l_0$.
$\ \ \ \ \$At $t_0$, the force $F_0$ at both ends of the spring is removed, particle $P$ moves with particle $A$, and particle $Q$ moves with particle $B$. At $t_1$, when the spring is in free length, particle $A$ and particle $P$ begin to separate, and particle $B$ and particle $Q$ begin to separate. Particle $A$ and particle $B$ move at velocity $u$ and $-u$ respectively. After that, spring $N$ and particle $P and Q$ vibrate freely.
$\ \ \ \ \$At $t_2$, when the spring is at the maximum extension length, apply force $F_2$ at both ends of the spring to make spring $N$ and particle $P and Q$ rest again, spring length $l_2$.
$\ \ \ \ \$ $l_2< l_0$，$F_2< F_0$.

$\ \ \ \ \$Before $t_0$, the energy of spring $N$ and particle $P and Q$is $m_2c^2$+$m_1c^2$, and the rest mass of particle $A$ and particle $B$ is $m_3$ respectively. Spring $N$ and particle $P and Q$ lose energy $m_1c^2$which is converted into the increased kinetic energy of particle $A$ and particle $B$.
$\ \ \ \ \$After $t_2$, the energy of particle $A$ and particle $B$ is $2m_3c^2$+$m_1c^2$, and the energy of spring $N$ and particle $P and Q$ is $m_2c^2$. Here $2m_3c^2$+$m_1c^2$$=\frac {2m_3c^2} {\sqrt {1-\frac {u^2} {c^2}} }$, get $\frac {m_3} {\sqrt {1-\frac {u^2} {c^2}} }$=${m_3} +\frac { m_1} 2$
$\ \ \ \ \$The inertial reference frame $K’$ moves at velocity $v$($v>0$) on the $x$direction relative to $K$.
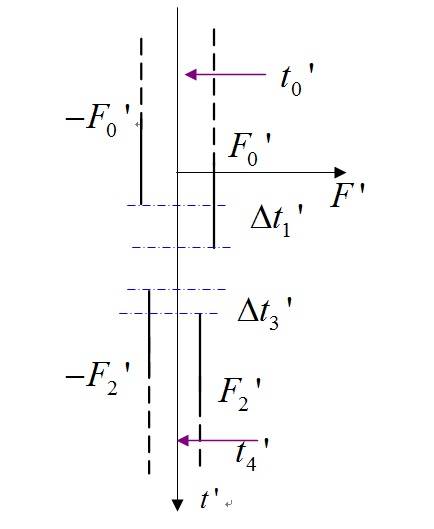
$\ \ \ \ \$In $K’$, the external force of the system is as shown in the figure, ${F_0}’ { \Delta t_1}’$$-{F_2}’ {\Delta t_3}’$>0. At ${t_0}’$,${t_4}’$, the momentum of the system ($x'$ direction) is different.

$\ \ \$But ${u_a}’=\frac { u -v} {1-\frac { u v } {c^2}}$ , ${u_b}’=\frac { -u -v} {1-\frac { u v } {c^2}}$
$\ \ \$$P_x({t_0}’) =\frac { -2m_3v-m_1v-m_2v } {\sqrt {1-\frac { v^2}{ c^2}}}$
$\ \ \$$P_x({t_4}’) =\frac { m_3} {\sqrt {1-\frac { {u_a}’^2}{ c^2}}} {u_a}’ +\frac { m_3} {\sqrt {1-\frac { {u_b}’^2}{ c^2}}} {u_b}’$ $-\frac {m_2v } {\sqrt {1-\frac { v^2}{ c^2}}}$
$\ \ \$$\sqrt {1-\frac { {u_a}’^2}{ c^2}}=$ $\frac {\sqrt {\left( 1- \frac { {u }^2}{ c^2} \right) \left( 1-\frac { v^2} { c^2} \right )}} {1-\frac { uv }{ c^2}}$
$\ \ \$$\frac {m_3} {\sqrt {1-\frac { {u_a}’^2}{ c^2}}} {u_a}’=$ $\frac { m_3 \left( 1-\frac { uv }{ c^2}\right) } {\sqrt {\left( 1- \frac { {u }^2}{ c^2} \right) \left( 1-\frac { v^2} { c^2} \right )}} \frac { u -v} {1-\frac { u v } {c^2}}$= $\left({ m_3+ \frac {m_1} 2 }\right) \frac { u -v} {\sqrt { 1-\frac { v^2} { c^2} }}$
$\ \ \$$\frac {m_3} {\sqrt {1-\frac { {u_b}’^2}{ c^2}}} {u_b}’=$ $\left({ m_3+ \frac {m_1} 2 }\right) \frac { -u -v} {\sqrt { 1-\frac { v^2} { c^2} }}$
$\ \ \$$P_x({t_0}’) = P_x({t_4}’)$
$\ \ \ \ \$At ${t_0}’$,${t_4}’$, the momentum of the system ($x'$ direction) is the same.
$\ \ \ \ \$What have I forgotten in this calculation?

 

[Vanadium 50]

Are you asking us to find your mistake in this wall of numbers?
Or are you suggesting relativity is inconsistent?

 

[Nugatory]

What have I forgotten in this calculation?

I’m not going to wade through that wall of text to see if these are the only problems, but I believe you’ve overlooked relativity of simultaneity (if both ends are at their extreme positions at the same time in one frame, they are not in any other frame) and that changes in the tension of the spring do not propagate instantaneously.

 

[pervect]

Summary:: The momentum calculated by two ways is inconsistent

What have I forgotten in this calculation?

If you want to get consistent answers, you'll need to add the contribution that tension in the string makes to the momentum and energy of the system. This is doe by using the stress-energy tensor.

https://en.wikipedia.org/w/index.php?title=Stress–energy_tensor&oldid=926066973

To understand the stress-energy tensor, it would be highly recommended to have some knowledge of tensors. Even with a background in tensors, you'll most likely need a textbook to fully understand how to work out your problem.

In units where c=1, called geometric units, and in 1+1 dimensoinal space time (one spatial dimension, one time dimension), we can intepret $T^{00}$ as the energy density per unit volume, $T^{01} = T^{10}$ (by symmetry) as the momentum density, and $T^{11}$ as the pressure in the spring (if it's negative, it will be a tension).

The key point to realize is that if you imagine the stress-energy tensor of a spring with negligible mass, in the rest frame of said spring the energy and momentum density is zero. It is not zero in a moving frame, by the way the stress energy tensor transforms.

As a rank 2 tensor, we can write

$$T^{cd} = \sum_{a,b} T^{ab} \Lambda ^c{}_a \Lambda^d{}_b$$

where $\Lambda$ is the Lorentz transformation matrix which transforms from one frame to another. In units where c=1, this is just

$$\Lambda^a{}_b = \begin{bmatrix} \gamma & -\gamma \beta \\ -\gamma \beta & \gamma \end{bmatrix}$$

where $\beta = v/c$ and $\gamma = 1 / \sqrt{1-\beta^2}$.

Expanding the summation over a and b in the first equation, out, we can expand the energy density $T'^{00}$ in a frame moving with a normalized velocity $\beta$ as:

$$T'^{00} = \Lambda^0{}_0 \Lambda^0{}_0 T^{00} + \Lambda^0{}_0 \Lambda^0{}_1 T^{01} + \Lambda^0{}_1 \Lambda^0{}_0 T^{10} + \Lambda^0{}_1 \Lambda^0{}_1 T^{11}$$

So we can see that if in some frame $T^{00} = T^{01} = T^{10} = 0$, but $T^{11}$ is not zero, representing a stretched or compressed spring, then the transformed energy density $T``'^{00}$ is not zero in the moving frame. even though we assumed it was zero in the stationary frame.

For this to have some intuitive significance, one needs to know that $T^{00}$ represents energy density per unit volume, $T^{01}=T^{10}$ represents momentum density, and $T^{11}$ represents pressure in the spring (if it's positive) or tension in the spring (if it's negative).

This is not particularly intuitive, and will require some serious study. In particular, some generally knowledge of the properties of all tensors is needed to understand the specifics of the particular tensor that is the stress-energy tensor.

 

[Dale]

Are you asking us to find your mistake in this wall of numbers?

@liuxinhua as @Vanadium 50 says, your post is very hard to read. Some specific suggestions:

1) Clearly define every variable used, do not expect others to infer it from context
2) Equations and computations should have brief explanations/justifications
3) Use natural units so that all factors of c can be removed
4) Clearly state your final concern

At ${t_0}’$,${t_4}’$, the momentum of the system ($x'$ direction) is the same.

What have I forgotten in this calculation?

If I am understanding your notation then you have shown that the total system momentum in the primed frame is the same before and after all of the interactions. This is expected, so I am not sure why you think that something has been forgotten.

 

[pervect]

In a previous post, I wrote:

$$T^{cd} = \sum_{a,b} T^{ab} \Lambda ^c{}_a \Lambda^d{}_b$$

where $\Lambda$ is the Lorentz transformation matrix which transforms from one frame to another. In units where c=1, this is just

$$\Lambda^a{}_b = \begin{bmatrix} \gamma & -\gamma \beta \\ -\gamma \beta & \gamma \end{bmatrix}$$

where $\beta = v/c$ and $\gamma = 1 / \sqrt{1-\beta^2}$.

Expanding the summation over a and b in the first equation, out, we can expand the energy density $T'^{00}$ in a frame moving with a normalized velocity $\beta$ as:

$$T'^{00} = \Lambda^0{}_0 \Lambda^0{}_0 T^{00} + \Lambda^0{}_0 \Lambda^0{}_1 T^{01} + \Lambda^0{}_1 \Lambda^0{}_0 T^{10} + \Lambda^0{}_1 \Lambda^0{}_1 T^{11}$$

I wanted to complete this, and write the equation I had in mind in terms of $\rho$, the energy density, which is $T^{00}$, p, the momentum density, which is $T^{01}=T^{10}$, and P, the pressure, which is $T^{11}$

We can then write

$$\rho' = \gamma^2 \rho - 2 \gamma^2 \beta p + \gamma^2 \beta^2 P$$

So the point is that $\rho$, p, and P do not transform in special relativity the way one would expect.

It might also be worthwhile looking at the case of an object where $\rho$ is non-zero, and p and P are both zero.

We can see that $\rho' = \gamma^2 \rho$. The factor of $\gamma^2$ may be unexpected, but the volume of the object does not stay constant between frames, due to Lorentz contraction the volume shrinks by a factor of $\gamma$ in the moving frame. When we account for this change in volume, we get for the total energy, E the integral of $\rho$, the energy density, over the volume

$$E' = \gamma E$$

Similarly, we would find the total momentum and the volume integral of p. I don't think it makes much physical sense to consdier the volume integral of P. It may make sense, but I'm not aware of how it might.

I also did not write out the transformation laws for p and P , using symbols, I only wrote them in tensor notation. Rewriting the tensor notation into the above symbols is left as an exercise for the reader.

 

[liuxinhua]

If I am understanding your notation then you have shown that the total system momentum in the primed frame is the same before and after all of the interactions. This is expected, so I am not sure why you think that something has been forgotten.

Because
From $l_2< l_0$，$F_2< F_0$, can get ${F_0}’> {F_2}’ ,{ \Delta t_1}’>{\Delta t_3}’$.

$\ \ \ \ \$In $K’$, the external force of the system is as shown in the figure, ${F_0}’ { \Delta t_1}’$$-{F_2}’ {\Delta t_3}’$>0. At ${t_0}’$,${t_4}’$, the momentum of the system ($x'$ direction) is different.

I’m not going to wade through that wall of text to see if these are the only problems, but I believe you’ve overlooked relativity of simultaneity (if both ends are at their extreme positions at the same time in one frame, they are not in any other frame) and that changes in the tension of the spring do not propagate instantaneously.

In fact, the different results of this momentum calculation are entirely due to the relativity of the same time.
I think so. But I'm afraid I made a mistake.

 

[liuxinhua]

 

[Dale]

Because
From $l_2< l_0$，$F_2< F_0$, can get ${F_0}’> {F_2}’ ,{ \Delta t_1}’>{\Delta t_3}’$.

In fact, the different results of this momentum calculation are entirely due to the relativity of the same time.
I think so. But I'm afraid I made a mistake.

The four momentum is the same before and after in the unprimed frame, so it must be the same before and after in all frames.

 

[liuxinhua]

The four momentum is the same before and after in the unprimed frame, so it must be the same before and after in all frames.

On the one hand, you agree that its momentum is the same at two times
By the following way, it can be obtained that its momentum is not the same at two times

$\ \ \ \ \$In $K’$, the external force of the system is as shown in the figure,

$\ \ \ \ \$Because
$\ \ \ \ \$${ \Delta t_1}’= \frac { \frac {v l_0} {c^2}} {\sqrt {1- \frac {v^2}{c^2}}}$
$\ \ \ \ \$${ \Delta t_3}’= \frac { \frac {v l_2} {c^2}} {\sqrt {1- \frac {v^2}{c^2}}}$
$\ \ \ \ \$From $l_2< l_0$， can get ${ \Delta t_1}’ >{\Delta t_3}’$.
$\ \ \ \ \$And $F_2< F_0$
$\ \ \ \ \$So ${F_0}’ { \Delta t_1}’$$-{F_2}’ {\Delta t_3}’$>0.

$\ \ \ \ \$At ${t_0}’$,${t_4}’$, the momentum of the system ($x'$ direction) is different.

 

[jartsa]

$\ \ \ \ \$From $l_2< l_0$， can get ${ \Delta t_1}’ >{\Delta t_3}’$.
$\ \ \ \ \$And $F_2< F_0$
$\ \ \ \ \$So ${F_0}’ { \Delta t_1}’$$-{F_2}’ {\Delta t_3}’$>0.

$\ \ \ \ \$At ${t_0}’$,${t_4}’$, the momentum of the system ($x'$ direction) is different.

Momentum of the system is different??

At this point of the story there were two opposing forces that stopped the two balls and the spring between them. So net change of momentum should be zero.

Oh I see, when the balls were stopped, the system of balls lost internal kinetic energy, so it lost momentum too, in all frames except in the rest frame of the system. So, in the frame of the spring there was no change of momentum of either of the two systems of balls.

But in frame K' the momentum of system of the balls that were stopped changed. But the momentum of system of the balls that were not stopped did not change. Is this perhaps the problem you are talking about?

 

[Dale]

By the following way, it can be obtained that its momentum is not the same at two times

Sure, that is during the time that the external forces on the system are changing in a spacelike fashion. That doesn’t change the fact that after the spacelike changes in external forces are complete the four-momentum is the same.

Also, $F\Delta t$ is not the change in the spatial component of the four momentum.

 

[vanhees71]

In a previous post, I wrote:
I wanted to complete this, and write the equation I had in mind in terms of $\rho$, the energy density, which is $T^{00}$, p, the momentum density, which is $T^{01}=T^{10}$, and P, the pressure, which is $T^{11}$

We can then write

$$\rho' = \gamma^2 \rho - 2 \gamma^2 \beta p + \gamma^2 \beta^2 P$$

So the point is that $\rho$, p, and P do not transform in special relativity the way one would expect.

It might also be worthwhile looking at the case of an object where $\rho$ is non-zero, and p and P are both zero.

We can see that $\rho' = \gamma^2 \rho$. The factor of $\gamma^2$ may be unexpected, but the volume of the object does not stay constant between frames, due to Lorentz contraction the volume shrinks by a factor of $\gamma$ in the moving frame. When we account for this change in volume, we get for the total energy, E the integral of $\rho$, the energy density, over the volume

$$E' = \gamma E$$

Similarly, we would find the total momentum and the volume integral of p. I don't think it makes much physical sense to consdier the volume integral of P. It may make sense, but I'm not aware of how it might.

I also did not write out the transformation laws for p and P , using symbols, I only wrote them in tensor notation. Rewriting the tensor notation into the above symbols is left as an exercise for the reader.

Also note that you can calculate the total energy and momentum in a naive way only when the energy-momentum tensor is divergence free, i.e., if it obeys the local conservation law
$$\partial_{\mu} T^{\mu \nu}=0,$$
because only then the naive definition of the energy-momentum vector
$$p^{\mu} =\int_{\mathbb{R}^3} \mathrm{d}^3 \vec{x} T^{\mu 0}(t,\vec{x})$$
is transforming like vector components (and is conserved).

 

[Vanadium 50]

1) Clearly define every variable used, do not expect others to infer it from context
2) Equations and computations should have brief explanations/justifications
3) Use natural units so that all factors of c can be removed
4) Clearly state your final concern

This.

I would add the following:

5) Reply on the thread; don't pester people via PM.
6) Use gamma notation
7) For heaven's sake, proofread your LaTex. It's riddled with errors. How do you expect us to find your mathematical errors if you aren't willing to remove the other errors?

 

[liuxinhua]

Also note that you can calculate the total energy and momentum in a naive way only when the energy-momentum tensor is divergence free, i.e., if it obeys the local conservation law

In$K'$ at time ${t_0}‘$ System $M$ is static.
In$K'$ at time ${t_4}‘$ System $M$, except particle $A$ and $B$, is static.

 

[liuxinhua]

Also, $F\Delta t$ is not the change in the spatial component of the four momentum.

$F\Delta t$ is not the change in the spatial component of the four momentum.
I didn't understand the meaning of the word $spatial component$.

You mean $F\Delta t$ is not the change of the four momentum in an inertial reference system?

 

[liuxinhua]

This.

I would add the following:

5) Reply on the thread; don't pester people via PM.
6) Use gamma notation
7) For heaven's sake, proofread your LaTex. It's riddled with errors. How do you expect us to find your mathematical errors if you aren't willing to remove the other errors?

Sorry

 

[Dale]

$F\Delta t$ is not the change in the spatial component of the four momentum.
I didn't understand the meaning of the word $spatial component$.

You mean $F\Delta t$ is not the change of the four momentum in an inertial reference system?

Hmm, it sounds like you are not familiar with four-vectors at all. In an inertial reference frame* you can write the coordinates of an event as a sort of vector with components $(ct,x,y,z)$, and in units where c=1 this becomes simply $(t,x,y,z)$. $t$ is the temporal or timelike component and $x,y,z$ are the spatial or spacelike components. From this you can define a notion of length in spacetime $d\tau^2=dt^2-dx^2-dy^2-dz^2=-ds^2$ and you can derive the Lorentz transform as the family of transformations that leaves the form of this length the same. The great thing about this approach is that it unifies many separate concepts. In particular, energy and momentum have the same relationship to each other as time and space, and the conservation of energy, momentum, and mass are seen to all be simply different facets of one overall conservation law: the conservation of four-momentum.

For further details see:
http://hyperphysics.phy-astr.gsu.edu/hbase/Relativ/vec4.html
https://en.wikipedia.org/wiki/Four-vector
https://en.wikipedia.org/wiki/Four-momentum

*in a more rigorous treatment you can drop the requirement for the reference frame to be inertial, but then coordinates themselves are not vectors but instead you use a set of basis vectors at each point which are derived from the coordinates. This distinction is not essential for a brief introduction to the topic.

 

[liuxinhua]

I get a general idea of what you mean. It can be concluded simply,

$\ \ \ \ \$At ${t_0}’$,${t_4}’$ in $K’$, the momentum of the system ($x'$ direction) is the same. This is a conclusion, called Conclusion 1.

But how to explain the following conclusion, called Conclusion 2? From ${t_0}’$,${t_4}’$ in $K’$, the accumulation of external force $F$ over time is not equal to 0, $\int_{{t_0}’}^{{t_4}’} F’ t’~dt ’$ $={F_0}’ { \Delta t_1}’$$-{F_2}’ {\Delta t_3}’$>0. At ${t_0}’$,${t_4}’$ in $K’$, the momentum of the system ($x'$ direction) is different.

 

[liuxinhua]

There was a writing error in the last post. Correct as follows,

From ${t_0}’$,${t_4}’$ in $K’$, the accumulation of external force $F'$ over time is not equal to 0, $\int_{{t_0}’}^{{t_4}’} F’(t’) ~dt ’$ $={F_0}’ { \Delta t_1}’$$-{F_2}’ {\Delta t_3}’$>0.
Conclusion 2， At ${t_0}’$,${t_4}’$ in $K’$, the momentum of the system ($x'$ direction) is different.
Conclusion 2 contradicts Conclusion 1.

 

[Dale]

At t0′,t4′ in K’, the momentum of the system (x′ direction) is the same. This is a conclusion, called Conclusion 1.

More importantly the four-momentum is the same. If the momentum is the same at t0 in one frame as it is at t4 then it may not be the same in all frames (at t0’ vs t4’). But if the four-momentum is the same in one frame then it will be the same in all frames.

the accumulation of external force F′ over time is not equal to 0

In relativity $F \Delta t$ is not equal to the change in momentum. The change in four momentum is given by the integral of the four force with respect to proper time.

 

[pervect]

The short version is that the Original Poster's handling of springs in special relativity isn't going to work for rather fundamental reasons. I did my best to point out some methods that might work, but they're probably too advanced. I hope what the OP takes away from this thread is that they don't yet know yet how to properly formulate springs and/or elastic media in the context of SR. I hope they focus on what they do have the background for, namely point particles, learn about those, and save the more advanced topics for a later date.

 

[pervect]

Also note that you can calculate the total energy and momentum in a naive way only when the energy-momentum tensor is divergence free, i.e., if it obeys the local conservation law
$$\partial_{\mu} T^{\mu \nu}=0,$$
because only then the naive definition of the energy-momentum vector
$$p^{\mu} =\int_{\mathbb{R}^3} \mathrm{d}^3 \vec{x} T^{\mu 0}(t,\vec{x})$$
is transforming like vector components (and is conserved).

I believe it is correct to say that as long as one considers the complete closed system, it's safe to say that $\nabla_a T^{ab}$ or, in the case of cartesian coordiniates, $\partial_a T^{ab}$ is zero, as energy-momentum is conserved.

If one has a mechanical system coupled with fields, and one ignores the fields, then the system won't be complete, and momentum and energy aren't conserved. One can think of this as an accounting error - there is energy and momentum being transferred from the mechanical system to the fields, and this isn't being accounted for.

That may be one way of looking at the original poster's issue with springs.

 

[pervect]

I did a google search for relativistic springs, and came up with a paper by Clark, https://arxiv.org/abs/1205.2823. I can't say for sure that Clark's approach will work, but it looks like it could work. It doesn't use a tensor formulation, so it might be more accessible than the stress energy tensor approach I suggested.
It's not published, but as someone's thesis paper it has apparently had at least some review by professionals. Google also mentions it's been cited four times.

I'll quote some of the bits I found interesting.

Chapter 2: Delayed Forcing

One of the most central ideas of special relativity is that nothing, not even informa-tion, can travel faster than the speed of light. The force lawused in the last chapter,F=−k x, assumes that the position information travels along the spring instanta-neously. We must modify it and delay the force law. We will do so by replacing theforce with the gradient of a retarded potential, similar to what is done in electromagnetism.

As is well known, the relativity of simlutaneity means that the notion of "at the same time" depends on the observer. This is most likely the cause of the OP's inconsitent results. The standard formulation of a spring as obeying Hooke's law is inherently non-relativistic because of this issue, unless adjustements are made.

A bit of caution from the paper I mentioned.

At the risk of sounding pedantic, we must make this clear: we are no longer describing the behavior of a true-to-life spring, in fact thissystem is a far cry from youreveryday slinky; we are simply describing two point masses interacting via a delayedspring potential. Accordingly we must check our intuition at the door. We will proceedby discussing the qualitative features of this system

 

[liuxinhua]

In relativity $F \Delta t$ is not equal to the change in momentum. The change in four momentum is given by the integral of the four force with respect to proper time.

I accept your opinion for the time being.
Thank you for your help.

And thanks Vanadium 50, Nugatory,pervect, jartsa, vanhees71.