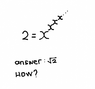- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Can someone solve this exponential equation for me?
- B
- Thread starter Ameer Bux
- Start date
In summary: So we only need to establish that is x^x^x^x...^x defined for x=\sqrt{2}I'm not sure what you're saying here.I was pointing out that, while it is true thatlimn→∞ xn = SimpliescS = S,it does not follow that any S satisfyingcS = Sis the limit of the xn.In fact, the limit of the xn for c = √2 is closer to 2.0000000000000004 than it is to 2.The point of the paragraph that is quoted is that the convergence range is not well-described by the argument that was given in the
Mathematics news on Phys.org
- #2
mgkii
- 138
- 42
Not totally sure I follow the logic here. It feels like it should be correct... but I'm going to have to read this a few more times! Taken from http://mathforum.org/
Dear Dr. Math,
What is the value of x in the following equation:
' ...
' x
' x
' x
' x
'x = 2
Thank you.
Benno
Date: 10/14/97 at 19:15:09
From: Doctor Tom
Subject: Re: algebra
There's a trick to solving this problem instantly. Since the exponents
go on forever, the exponent of the lowest and leftmost x is the same
as x to that power, so replace the equation by
2
x = 2
So x is the square root of 2, or 1.4142135...
Dear Dr. Math,
What is the value of x in the following equation:
' ...
' x
' x
' x
' x
'x = 2
Thank you.
Benno
Date: 10/14/97 at 19:15:09
From: Doctor Tom
Subject: Re: algebra
There's a trick to solving this problem instantly. Since the exponents
go on forever, the exponent of the lowest and leftmost x is the same
as x to that power, so replace the equation by
2
x = 2
So x is the square root of 2, or 1.4142135...
- #3
TeethWhitener
Science Advisor
Gold Member
- 2,618
- 2,228
Plug in ##\sqrt{2}## for ##x## and solve for ##y## like so:
$$y = \sqrt{2}^{\sqrt{2}^\ldots}$$
Since the power tower goes to infinity, this is equivalent to:
$$y=(\sqrt{2})^y$$
Do you see why? Now solve for ##y##. (Or if you like, just plug in ##y=2## and verify that the equation is true.)
$$y = \sqrt{2}^{\sqrt{2}^\ldots}$$
Since the power tower goes to infinity, this is equivalent to:
$$y=(\sqrt{2})^y$$
Do you see why? Now solve for ##y##. (Or if you like, just plug in ##y=2## and verify that the equation is true.)
- #4
BvU
Science Advisor
Homework Helper
- 15,979
- 4,806
[edit] I goofed here! see further down...
Well, I think you have a problem. Since $$\left (\left ( \sqrt 2 \right )^\sqrt 2 \right )^\sqrt 2 = 2 $$ I think it should stop at $$ 2 = x^{x^x}$$
You are being lured into the reasoning of post #2, but it's a circular reasoning: IF $$2 = 2^{x^{x^{x^{x^{x^{x^{x^{...}}}}}}}} $$ THEN x =2 . If not, then not!
Well, I think you have a problem. Since $$\left (\left ( \sqrt 2 \right )^\sqrt 2 \right )^\sqrt 2 = 2 $$ I think it should stop at $$ 2 = x^{x^x}$$
You are being lured into the reasoning of post #2, but it's a circular reasoning: IF $$2 = 2^{x^{x^{x^{x^{x^{x^{x^{...}}}}}}}} $$ THEN x =2 . If not, then not!
Last edited:
- #5
TeethWhitener
Science Advisor
Gold Member
- 2,618
- 2,228
BvU said:Well, I think you have a problem. Since $$\left (\left ( \sqrt 2 \right )^\sqrt 2 \right )^\sqrt 2 = 2 $$ I think it should stop at $$ 2 = x^{x^x}$$
You are being lured into the reasoning of post #2, but it's a circular reasoning: IF $$2 = 2^{x^{x^{x^{x^{x^{x^{x^{...}}}}}}}} $$ THEN x =2 . If not, then not!
The problem here is that
$$((\sqrt{2})^{\sqrt{2}})^{\sqrt{2}} \neq \sqrt{2}^{\sqrt{2}^{\sqrt{2}}}$$ because exponentiation is not associative.
- #6
BvU
Science Advisor
Homework Helper
- 15,979
- 4,806
Ah! It's me making the mistake ? What are the conventions then to interpret ##
\sqrt{2}^{\sqrt{2}^{\sqrt{2}}} ## ?
Got it !
From here :
\sqrt{2}^{\sqrt{2}^{\sqrt{2}}} ## ?
Got it !

From here :
And I was just as dumb as XL...Without parentheses to modify the order of calculation, by convention the order is top-down, not bottom-up:
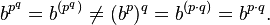
Note that some computer programs (notably Microsoft Office Excel) associate to the left instead, i.e. a^b^c is evaluated as (a^b)^c.
Last edited:
- #7
TeethWhitener
Science Advisor
Gold Member
- 2,618
- 2,228
Maybe it's different for you, but I've always seen
$$\sqrt{2}^{\sqrt{2}^{\sqrt{2}}} = \sqrt{2}^{\bigg(\sqrt{2}^{\sqrt{2}}\bigg)} $$
It's too early for this much nested LaTeX.
$$\sqrt{2}^{\sqrt{2}^{\sqrt{2}}} = \sqrt{2}^{\bigg(\sqrt{2}^{\sqrt{2}}\bigg)} $$
It's too early for this much nested LaTeX.
- #8
BvU
Science Advisor
Homework Helper
- 15,979
- 4,806
Yeah, it is. (here it is too late, actually -- time to go home  ).
).
But thanks for puttingus me right !
But thanks for putting
- #9
Martin Rattigan
- 330
- 3
The "trick" mentioned by Dr. Tom does in this instance give a correct solution, but it's not a proof. As mentioned by Peter Winkler in his book "Mathematical Puzzles" one has only to consider the similar equation [tex]x^{x^{x^{.^{.^.}}}}=4[/tex]
Using the same logic gives [itex]x^4=4[/itex], i.e. [itex]x=\sqrt{2}[/itex]. If the "proof" were correct we would then have [tex]2=\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{.^{.^.}}}}=4[/tex]
(Not to mention that [itex]x^2=2[/itex] actually has two solutions.)
Using the same logic gives [itex]x^4=4[/itex], i.e. [itex]x=\sqrt{2}[/itex]. If the "proof" were correct we would then have [tex]2=\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{.^{.^.}}}}=4[/tex]
(Not to mention that [itex]x^2=2[/itex] actually has two solutions.)
Last edited:
- #10
zinq
- 399
- 119
If a tower of exponentials, defined as the limit of xn as n → ∞, where for some real c > 0 we define
actually converges, then it can be proved that c satisfies the inequality
(where e is the famous mathematical constant e = 2.718281828...) or in decimals,
and in fact xn will converge for all such c.
It's rather unusual to have a situation like this where the endpoints of the region of convergence are included in the region of convergence!
It's not hard to show that, if we do have convergence to some number S = S(c):
then we must also have
as suggested above. But, this does not mean that any S satisfying the above equation is necessarily the limit of the xn.
So in particular, the fact that the 4th power of √2 is 4 does not mean that 4 is the limit of the xn for the value c = √2. It most certainly is not.
In fact, it is known that for the lower end of the range of c that gives a convergent tower, we have:
and at the high end, we have:
These facts rule out, for instance, the possibility that for c = √2 we have S = 4.
x1 = c
and
xn+1 = cxn,
actually converges, then it can be proved that c satisfies the inequality
e-e ≤ c e1/e,
(where e is the famous mathematical constant e = 2.718281828...) or in decimals,
0.065988... ≤ c ≤ 1.444667...,
and in fact xn will converge for all such c.
It's rather unusual to have a situation like this where the endpoints of the region of convergence are included in the region of convergence!
It's not hard to show that, if we do have convergence to some number S = S(c):
limn→∞ xn = S
then we must also have
cS = S,
as suggested above. But, this does not mean that any S satisfying the above equation is necessarily the limit of the xn.
So in particular, the fact that the 4th power of √2 is 4 does not mean that 4 is the limit of the xn for the value c = √2. It most certainly is not.
In fact, it is known that for the lower end of the range of c that gives a convergent tower, we have:
for c = e-e, S = 1/e,
and at the high end, we have:
for c = e1/e, S = e.
These facts rule out, for instance, the possibility that for c = √2 we have S = 4.
- #11
Martin Rattigan
- 330
- 3
I was actually playing Devil's advocate to point out that there was something missing from the original logic.
I did prove that [itex]\lim_{n \to \omega}(\sqrt{2} \uparrow\uparrow n)=2[/itex] without establishing the convergence range you give. The solution [itex]x=-\sqrt{2}[/itex] also needs to be discounted.
I did prove that [itex]\lim_{n \to \omega}(\sqrt{2} \uparrow\uparrow n)=2[/itex] without establishing the convergence range you give. The solution [itex]x=-\sqrt{2}[/itex] also needs to be discounted.
Last edited:
1. How do I solve an exponential equation?
To solve an exponential equation, you can use logarithms. Take the logarithm of both sides of the equation, then use the properties of logarithms to simplify the equation and solve for the variable.
2. What is the general strategy for solving an exponential equation?
The general strategy for solving an exponential equation is to isolate the exponential term on one side of the equation, take the logarithm of both sides, use the properties of logarithms to simplify the equation, and then solve for the variable.
3. Can all exponential equations be solved?
Not all exponential equations can be solved algebraically. Some equations may require the use of advanced techniques or numerical methods to find a solution.
4. Are there any special cases when solving exponential equations?
Yes, there are special cases when solving exponential equations, such as when the exponential term has a base of 1 or when the exponent is a negative number.
5. Can you provide an example of solving an exponential equation?
Yes, for example, to solve the equation 2^x = 8, we can take the logarithm of both sides: log(2^x) = log(8). Using the property of logarithms, we can rewrite the equation as x*log(2) = log(8). Then, we can solve for x by dividing both sides by log(2): x = log(8)/log(2). Therefore, x = 3 is the solution to the equation.
Similar threads
-
General Math
- Replies
- 1
- Views
- 667
-
General Math
- Replies
- 6
- Views
- 1K
-
General Math
- Replies
- 3
- Views
- 809
-
General Math
- Replies
- 2
- Views
- 993
-
General Math
- Replies
- 22
- Views
- 551
-
General Math
- Replies
- 3
- Views
- 1K
-
General Math
- Replies
- 2
- Views
- 1K
-
General Math
- Replies
- 2
- Views
- 1K
-
Differential Equations
- Replies
- 7
- Views
- 1K
- Replies
- 3
- Views
- 1K
Share: