JolileChat
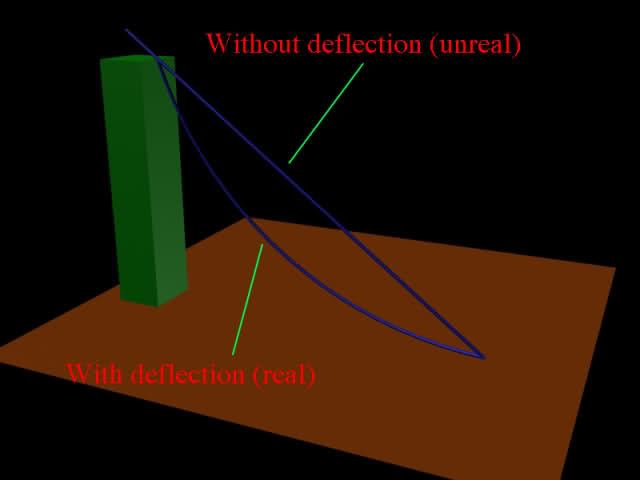
You will need to consider the inclination of the rod
Let’s assume that angle of inclination is 45 degrees

You will need to find out the equation of the elastic line of your beam
A good startup is: http://www.efunda.com/formulae/solid...ams/theory.cfm
There are three options under title Choose a Boundary Condition and Calculate!:
1.Cantilevers
2.Mixed (Fixed-Simple)
3.Simply Supported
I think that the third one is the most suitable for me, so chose that one and then several other options appeared:
1.Center Load
2.Intermediate Load
3.Two Equidistant Loads
4.Uniform Load
I think that the last one is most suitable in spite of the fact that there is no load-just uniform rod, so I chose that one and the calculator appeared there (
http://www.efunda.com/formulae/solid_mechanics/beams/casestudy_display.cfm?case=simple_uniformload), I put some values there:
Length of beam, L-Let it be 1 000 meters.
Line pressure load on beam, p: as I know in my case it will simply be the weight per meter length. So, if my rod’s radius is 1 meter then the volume of rod’s this part would be 3.14 m^3. As for its mass, if I use Carbon nanotubes their density varies between these values: 0.037-1.34 g/cm^3 (
http://en.wikipedia.org/wiki/Specific_strength). Let’s take some medium value-0.1 g/cm^3, so the mass of that part will be 314 kg. But how can I transform this value to Pa-m?
Young's Modulus, E: for Carbon nanotubes is equal to 1 000 GPa
http://en.wikipedia.org/wiki/Young's_modulus
Distance from neutral axis
to extreme fibers-as I know this will be the radius of the rod-1 meter
Moment of Inertia, I: it is equal to (pi*r^4)/4, so it is equal to 0.785
But my rod is inclined by 45 degrees, what should I do with this circumstance? :shy: