Can we take the partial derivatives of φ and ψ here?

[requied]

Homework Statement

Show that the function u=φ(xy) +√xy ψ(y/x)provides the following equation.

Relevant Equations

u=φ(xy) +√xy ψ(y/x)

I research about coordinate systems and I found the following informations about transformation.

Now, if I replace arctan (x/y) (according to the picture above) to φ, I think I can solve. But if I can do this, then what will be replaced to ψ? I mean, I know just taking partial derative about this question and I guess this symbols can look familiar someone who spend some times about the topic. I left below a clear picture of question. Thanks for now.

 

[BvU]

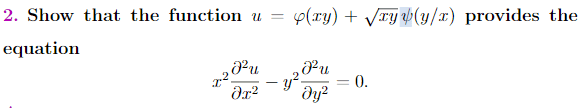
Now, if I replace arctan (x/y) (according to the picture above) to φ

Why do you think there is a relationship between the $\phi$ in the illegible picture and $\phi(xy)$ ?
And what about $\psi$ ?

What does your textbook mean if it asks to 'provide' something ?

$\$

My strong impression is that you are supposed to work out the partial derivatives. Do you know how to do that ?

 

[requied]

Why do you think there is a relationship between the ϕϕ\phi in the illegible picture and ϕ(xy)ϕ(xy)\phi(xy) ?
And what about ψψ\psi ?

I have told you that I have had no idea about these two symbols.

What does your textbook mean if it asks to 'provide' something ?

It is expected to prove if you're talking about it. Actually I don't get what you said.

 

[requied]

My strong impression is that you are suppsoed to work out the partial derivatives. Do you know how to do that ?

Yea I know how to do but I can't take derivative if I am not sure whether one each these symbols are equations. If these are constants, then there is no problem. I wondered if these are constant or not.

 

[BvU]

whether one each these symbols are equations

They are functions. Start working out $\partial \phi\over \partial x$ and post your work.

 

[BvU]

Actually I don't get what you said.

A more understandable wording would be "Show that $u = ...\$ satisfies the equation ..."

 

[requied]

A more understandable wording would be "Show that $u = ...\$ satisfies the equation ..."

Yea, he don't like speaking understandably :/

 

[requied]

They are functions. Start working out $\partial \phi\over \partial x$ and post your work.

Could you want to say $\partial \ u\over \partial x$ ?

 

[BvU]

Could you want to say $\partial \ u\over \partial x$ ?

​

No. You have to start somewhere. Function $u = \phi\ + ... \$, so ${\partial \ u\over \partial x} = {\partial \phi \over \partial x} \;+ ...$​

 

[BvU]

I was so eager to give you the easiest possible start with this assignment that I overlooked that it might still be unclear to you. What I meant may become clear when I hand you the first step as an example:

$${\partial \phi \over \partial x} = {\partial \phi(xy) \over \partial (xy)} \ {\partial (xy) \over \partial x} = \phi' \;y $$Now, this one is easy and you already see some possible cancelling come up in the second derivatives .

$\sqrt{xy}\;\psi(y/x)\$ is a little more work but the idea is the same (cross fingers...)

 

[requied]

I would have write ∂ϕ like that;
∂ϕ = ∂(u /(xy) +√xy ψ(y/x) )
Where did

(xy)

and

∂(xy)

come from?

 

[Delta2]

This is quite tricky problem. The "long and hard" way for this problem would be to set $z=xy,w=\frac{y}{x}$ and then to consider the function $$u(z,w)=\phi(z)+\sqrt{z}\psi(w)$$ and then calculate the derivatives $\frac{\partial u}{\partial z},\frac{\partial u}{\partial w}$ and then calculate the partial derivatives $\frac{\partial u}{\partial x},\frac{\partial u}{\partial y}$ using the 2-variable chain rule (for example $$\frac{\partial u}{\partial x}=\frac{\partial u}{\partial z}\frac{\partial z}{\partial x}+\frac{\partial u}{\partial w}\frac{\partial w}{\partial x}$$.

But this is the long , hard and painful way, the way @BvU suggests at post #10 is a clever shortcut. According to BvU's way you just have to know how to cleverly use the 1-variable chain rule.

 

[BvU]

I would have write ∂ϕ like that;
∂ϕ = ∂(u /(xy) +√xy ψ(y/x) )

That is not correct.

Where did $(xy)$ and $\partial \over\partial(xy)$ come from?

From your post #1:

$xy$ is the (single) argument of the function $\phi$. If I give you the value of $xy$, then you can give the value of $\phi(xy)$ if you know the function (which you don't).

My writing ${\partial\phi(xy)\over \partial(xy)}\equiv \phi'$ is just a sloppy physicist's way of avoiding to introduce a new variable, e.g. $z(x,y) = xy\$, but it comes down to the same thing:$${\partial \phi \over \partial x} = {\partial \phi \over \partial z} \ {\partial z \over \partial x} = \phi' \;y$$ -- the chain rule, as @Delta2 already said.

---

Yea I know how to

Can you give us an example that demonstrates that ? Not to be obnoxious, but to understand what assistance is most effective.

 

[requied]

I can't give an example because of it doesn't make sense to me.

I was so eager to give you the easiest possible start with this assignment that I overlooked that it might still be unclear to you. What I meant may become clear when I hand you the first step as an example:

$${\partial \phi \over \partial x} = {\partial \phi(xy) \over \partial (xy)} \ {\partial (xy) \over \partial x} = \phi' \;y $$Now, this one is easy and you already see some possible cancelling come up in the second derivatives .

$\sqrt{xy}\;\psi(y/x)\$ is a little more work but the idea is the same (cross fingers...)

I guess I found $\partial Ψ$/ $\partial \ y$. But I don't get why we are doing these calculations somehow. The question asks for $\partial \ u$/ $\partial \ x$ etc.

 

[requied]

Why we don't study on the calculation like that?

 

[BvU]

We do: $\ u = \phi + \psi\$, so your first factor is a $\;1\;$.

But in your post #15 you have completely forgotten $\;{\partial \psi\over \partial x}\;$ ?!

 

[requied]

We do: $\ u = \phi + \psi\$, so your first factor is a $\;1\;$.

But in your post #15 you have completely forgotten $\;{\partial \psi\over \partial x}\;$ ?!

I'll be hanged if I understand! Pardon but I'm just not be able to do these calculations. I'll glance at chain rule of partial derivatives. I guess we couldn't make progress.

 

[BvU]

I'll be hanged if I understand! Pardon but I'm just not be able to do these calculations.

Don't give up. We'll switch gear and try again. Since $$u = \phi + \sqrt{xy}\;\psi $$ we get $$
{\partial u\over \partial x} = {\partial\phi \over \partial x} + {\partial \sqrt{xy}\;\psi \over \partial x}$$
so ${\partial u\over \partial x}$ has two terms and we started with the first:$$
{\partial u\over \partial x} = {\partial\phi \over \partial x} + ...$$

There are a few simple rules underlying all this. Hang on a little more and you'll be allright.
Sloppy physicist's notation (consult calculus textbook for more):

Simple derivative: $$f(x)\quad\Rightarrow\quad df = {\partial f\over\partial x} \;dx $$

Two variables: $$f(x,y)\quad\Rightarrow\quad df = {\partial f\over\partial x} \;dx + {\partial f\over\partial y} \;dy $$

Change in sum = sum of changes:
$$\ u = \phi + \chi\quad
\Rightarrow \quad du = d\phi + d\chi\ $$
Clear enough, right ?

Product rule:
$$\ y = ab\quad\Rightarrow\quad dy = a\; db + b \; da$$
Also clear enough, right ?

Chain rule:
$$\ y = f\bigl (g(x)\bigr ) \quad\Rightarrow\quad dy = {\partial f\over\partial g} \;dg $$

A little more abstract! Example:
$$\ f = 1/g \quad\Rightarrow\quad df = {\partial f\over\partial g} \;dg \ = \ -{1\over g^2}\; dg$$

I'll be hanged if I understand!

Doesn't help me to help you. More useful to indicate where and how you get stuck: give an example of what you (just) understand and what about the next step you do not understand -- and why not.

(Easy to say for me, I grant you; not so easy for you -- but you are the asking party at this point )

If the above are sufficiently clear, we can go back to pick up at the point where we were before. OK ?

 

[requied]

I was studying on partial derivatives, chain rule etc uptill now. Deadline of the homework is tomorrow night. I guess I will not be able to complete the homework. If someone would give me the solution I really appreciate it. Else I will quit the question. I know that here is not a question solving site but I have to ask for it please forgive me. By the way, thanks a lot to @BvU and @Delta2. They supported me a lot.

 

[BvU]

If someone would give me the solution I really appreciate it

PF isn't in favour of just giving solutions -- our rules forbid it and it isn't very helpful for the receivers either. Pity about the deadline -- perhaps you get some help on Tuesday -- but if you don't get enough from teacher we can always continue unraveling the exercise with you.

 

[WWGD]

A way of doing it I thought was nice was to set up a path diagram between your initial function and the variables against which you differentiate.

 

[haruspex]

View attachment 264339

No.
Think of $\psi$ as a function of z, where z happens to equal xy always.
So $\psi$ is a function of only one variable, and $\psi'$ means the (normal, not partial) derivative of $\psi$ wrt that variable.
To get the partial derivative wrt x we use the chain rule:
$\frac{\partial \psi}{\partial x}=\frac{d\psi}{dz}\frac{\partial z}{\partial x}=\psi'\frac{\partial z}{\partial x}=\psi'\frac{\partial (xy)}{\partial x}=\psi'y$

The result to be proved in this thread is interesting. The general form that satisfies it is $u=x^ay^b\psi(x^cy^d)$ where either {a=b and c=d} or {a+b=1 and c=+/-d}.

 

[BvU]

I think @haruspex means $\phi$, not $\psi$ .

We had (in post #1) $$u(x,y)\equiv \phi(xy) + \sqrt{xy} \; \psi\left (y\over x\right )$$

On the other hand I did use partials in #10: $${\partial \phi \over \partial x} = {\partial \phi(xy) \over \partial (xy)} \ {\partial (xy) \over \partial x} = \phi' \;y $$ where I should (could ?) have used $\displaystyle {{\text d} \phi(xy) \over {\text d}xy}$ as @haruspex noted. That would have been more clear.