A Canonical transformation - derviation problem

[Vicol]

Let me show you part of a book "Mechanics From Newton’s Laws to Deterministic Chaos" by Florian Scheck.

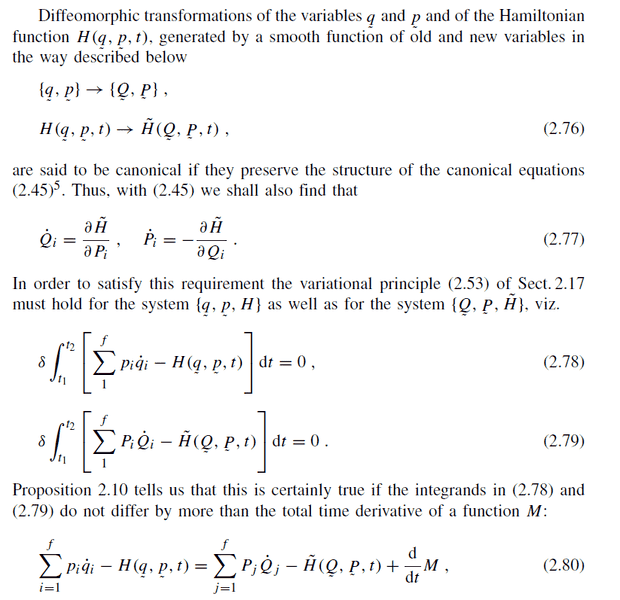
I do not understand why these integrands can differ by more than time derivative of some function M. Why doesn't it change the value of integrals?

It seems this point is crucial for me to get into generating functions (and then to Hamilton-Jacobi functions) but I won't proceed until I fully understand derviations. So can anyone explain mathematical story of the derviation?

 

[andrewkirk]

The claim depends on Proposition 2.10 so it is more likely that help can be provided if you can show Proposition 2.10.

 

[Vicol]

 

[singularity38]

That's because the Hamiltionian function is defined as the "Legendre Transformation" of the Lagrangian function or, in practice:

$$H = \sum \frac{\partial L}{\partial \dot{q_i}} \dot{q_i} - L $$ so the integrand function in (2.78) is nothing but the Lagrangian function. As you should know and as the proposition 2.10 says (and proves!) adding the total time derivative of a function $M(q,t)$ to the Lagrangian does not affect the motion described by the Lagrangian itself. You can visualize it by this way:

Let $L(q, \dot{q}, t)$ be a Lagrangian function, we now define $L'(q, \dot{q}, t)= L(q, \dot{q}, t) + \frac{dM(q,t)}{dt}$. We define the action as
$$ S' = \int_{t_1} ^{t_2} L'(q,\dot{q}, t)dt = \int_{t_1} ^{t_2} L(q,\dot{q}, t) dt + \int_{t_1} ^{t_2} \frac{dM(q,t)}{dt} dt = S + M(q_2,t_2) - M(q_1,t_1) = S + constant$$
where clearly $S= \int_{t_1} ^{t_2} L(q,\dot{q}, t)dt$. Now you can se that the condition $\delta S' = 0$ is perfectly equivalent to $\delta S=0$.