NewEngineer
- 21
- 2
To simplify my situation, I am installing a horizontal cantilever pipe (30” length, 3” nominal diameter) which will be connected to a vertical pipe (3” nom diameter, acting as the wall) by a T-connection. See the diagram below. At the end of the cantilever the pipe bends up at 90 degrees for 12”. At the top of the vertical pipe (at the end of the cantilever) will be a device (weight approx. 10 Lb = 4.53592 kg). The cantilever assembly pipe is most likely carbon steel, thickness 0.2159” (based on a 3” nominal diameter steel pipe schedule 40).
What I want to know is given these conditions, do I need to install a vertical support (under point B) for the extended pipe or would the pipe hold fine here? I’ve calculated the moment at point A as -95.922 lb*ft. If you look at the FBD you can see how I modeled the problem. I summed the forces of the Mass (M) and the vertical piece of pipe (MBC).
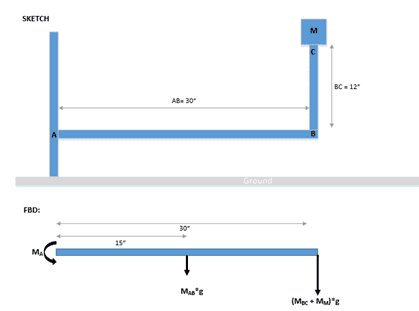
What I want to know is given these conditions, do I need to install a vertical support (under point B) for the extended pipe or would the pipe hold fine here? I’ve calculated the moment at point A as -95.922 lb*ft. If you look at the FBD you can see how I modeled the problem. I summed the forces of the Mass (M) and the vertical piece of pipe (MBC).