Dcus
- 4
- 0
Hi! I have the following question:
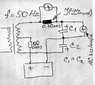
A capacitor is connected to a transformer(sine wave) with 5v of output voltage(RMS). What final voltage is applied to the capacitor plates? And should I consider the current applied to the capacitor equal to RMS value or double RMS value? Thanks.
A capacitor is connected to a transformer(sine wave) with 5v of output voltage(RMS). What final voltage is applied to the capacitor plates? And should I consider the current applied to the capacitor equal to RMS value or double RMS value? Thanks.