Capacitor's Charge distribution

[zorro]

Homework Statement

2 capacitors C1 = 4 and C2 = 6 are connected to a battery of emf V=12V in parallel. The battery is disconnected and the capacitors are rearranged in series. Find out the final charges on the capacitors.

The Attempt at a Solution

Why doesn't the charge conservation principle hold here?
i.e. (Q1 + Q2)V = Q1'V1 + Q2'V2

Does the charge (electric energy) get converted into heat?

 

[gneill]

What makes you think that charge conservation is not holding? What values do you get for the charge on each capacitor in their two arrangements?

 

[zorro]

I got the charges as 9.6 and 14.4 (in micro coulumbs) whose sum 24 is not equal to initial 120.

 

[gneill]

Each capacitor, taken in isolation, is a net neutrally charged object. The equal and opposite charges on their plates will greedily hang on to each other across the plate separation, so the charges "live" there on the inside plate surfaces.

When you stack two neutral objects, there is no current flow between them; The charges on their plates just stay where they were. In order get a flow of current, you'd have to provide a circuit, i.e., connect their other ends together as well, giving the charges on the plates another, lower potential target via their connecting leads..

The upshot of all this is that the capacitors should have the same charge on them as they did before they were connected end to end.

A nifty result is that the effective potential across the two outer ends has been doubled. This in fact is the basis of a very handy circuit called a voltage doubler, which, using alternating current and a few diodes, alternately charges in parallel and then connects in series a pair of capacitors, which are then then presented to the load as a doubled voltage source.

 

[zorro]

Initial potential across the capacitors = 12V
Final potential = V1 + V2= 4.8V

Voltage got doubled??

 

[gneill]

I didn't say that your answer was correct.

 

[zorro]

lol...you did not say that it is incorrect either
I can't find any mistake in my calculations.
What answer did you get?

 

[Piyu]

Can't seem to work this out, been trying for a while. In the end i always just end up with a ratio of the charges between 3/2(as according to the capacitance.

My mental image is there's 3 parallel lines, 2 with the capacitors and one with the battery. Then the battery is removed leaving the 2 capacitors in series in a loop.

In that case, won't the postive side remain as positive since there's no electrons to move around? And by this logic, the electrons on the other side should also be unchanged.

 

[gneill]

lol...you did not say that it is incorrect either
I can't find any mistake in my calculations.
What answer did you get?

If no current can flow because there's no complete circuit, and the charges on the capacitors have no incentive to move or leave their places on the plates, what should the charges on the capacitors be? How about the voltages?

 

[rl.bhat]

I got the charges as 9.6 and 14.4 (in microcoulombs) whose sum 24 is not equal to initial 120.

When you connect the capacitors in series, I hope, they are isolated.
In that case total charge will not leave the system. Two middle plates will acquire + 24 μC if the charges are free to move. What about the charges on the outer plate? Will the system act like a capacitor?
If the outer plates are grounded, excess charges on the outer plates will go to the ground.
Can you show your calculations?

 

[zorro]

There is a complete circuit.
They are connected in series circuit (sorry, 'rearranged' might be misleading)!

 

[Piyu]

In that case, won't the first part of the question be redundant? since the charges are going to get re-shuffled by the new emf in a series?

 

[gneill]

There is a complete circuit.
They are connected in series circuit (sorry, 'rearranged' might be misleading)!

Ah! Well that's a very different question then!

With a circuit in place, capacitor charges and potentials can change. The series capacitors have their "outer ends" connected, so the circuit is equivalent to the capacitors being connected in parallel with their (originally) +/- ends interchanged. You get partial charge cancellation. 72 - 48 = 24 microcoulombs remain after cancellation, spread over capacitance C1+C2.

24 µC / 10 µF = 2.4 V

 

[zorro]

@Piyu
There is no battery connected in second combination (read the q again, 'the battery is disconnected').

@gneill
Thats the way I did.
What charge distribution did you get?

 

[gneill]

Since the voltage across the two must be the same (they are in parallel), then just use the formula V = Q/C for each.

 

[hikaru1221]

Perhaps this picture may clear up the confusion?

 

[zorro]

I already drew that figure
The final charge distribution is 9.6 and 14.4 (in micro coulumbs), whose sum does not equal the initial total charge (120 microC). If it is right then why is the charge not conserved.

 

[hikaru1221]

I already drew that figure
The final charge distribution is 9.6 and 14.4 (in micro coulumbs), whose sum does not equal the initial total charge (120 microC). If it is right then why is the charge not conserved.

Which case are you referring to? 1 or 2? (see my picture)

 

[zorro]

Its the circuit's picture
Figure 2 (final charge distribution) which is 9.6 and 14.4 (micro C)

 

[gneill]

Charge is conserved. It's just that some of the electrons have found homes with some of the atoms that were previously missing them (the + charges).

When we say that a capacitor has Q coulombs stored, there's +Q coulomb's worth of deficit of electrons on one (each missing electron is one + charge), and -Q coulombs worth of surplus electrons on the other. Draw a gaussian surface around the device and it will show a net external field of zero, so no net charge on the whole device.

So before reconnection, both capacitors have a net zero total charge. It's just that they're holding some of their + and - charges apart from each other, separated by the distance between the plates. When you reconnect them, there is an opportunity for some of those unlike charges to get together and cancel, driven by the different voltage potentials that the capacitors start out with. Eventually both capacitors end up with the same potential across them (the same voltage) and the remaining free charges stop moving.

 

[hikaru1221]

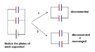
Its the circuit's picture
Figure 2 (final charge distribution) which is 9.6 and 14.4 (micro C)

So you are referrring to case 2? (the lower "disconnected + rearranged" circuit)

Anyway, I think there is one subtle mistake. Let me take an example. You connect a capacitor to the source, then disconnect the source and connect the 2 ends of the capacitor to each other. So now, the charge of capacitor is 0! How is the law of charge conservation "violated"?

It isn't. Actually, when we say "charge of capacitor" Q, it doesn't mean that Q is the net charge of the capacitor. Q is the charge on the positive plate of the capacitor, and so, the negative plate is -Q. The net charge of the capacitor is 0, and it always is! That's why when you connect the 2 ends, Q and -Q join each other, and you have 0 charge on the positive plate, i.e. "charge of capacitor" is 0.

Apply this to your problem. When you rearrange the capacitors like in case 2, the positive plate of one capacitor is connected to the negative plate of the other, and therefore, some (but not all) charges, both postive and negative, join and cancel out. That reduces the charges of positive plates of the 2 capacitors, i.e the charges of the capacitors.

P.S.:
_ The law of charge conservation applies to real charges, or the real phenomenon.
_ The "charge of capacitor" is just a convention and so is not the real phenomenon.

 

[ehild]

Perhaps this picture may clear up the confusion?

The problem said that the capacitors were rearranged in series. What does series connection mean?


ehild

 

[zorro]

@gneill and hikaru1221
Thank you for clearing my confusion

@ehild
Read my post #11

 

[ehild]

What is the difference between parallel and series if there is nothing else but two capacitors?

ehild

 

[zorro]

In parallel connection of two capacitors, the positive plates are connected together and the negative plates are connected together.

In series connection, the positive plate of one capacitor is connected to the negative plate of the other capacitor.

Refer Hikaru's figures 1 (parallel) and 2 (series)

P.S.- 'Series and Parallel' might not be the right terminology here.

 

[gneill]

In parallel connection of two capacitors, the positive plates are connected together and the negative plates are connected together.

In series connection, the positive plate of one capacitor is connected to the negative plate of the other capacitor.

Refer Hikaru's figures 1 (parallel) and 2 (series)

P.S. 'Series and Parallel' might not be the right terminologies.

Nope. Not the right terminology for what you're trying to convey. The capacitors in this problem are definitely in parallel at the start and again at the finish!

 

[hikaru1221]

We have a semantic problem here.

 

[zorro]

Nope. Not the right terminology for what you're trying to convey. The capacitors in this problem are definitely in parallel at the start and again at the finish!

But in the middle they are in series. You can't express the reconnection as 'parallel combination' as they were already in parallel. Once connected in series, the charges re-distribute and we get parallel combination.

I think 'series' and 'parallel' connection are meaningless once the battery has been disconnected.

 

[gneill]

Parallel connection means that each of the two leads of one component is connected to to one (different) lead of the other component. Their leads are connected pairwise.

If one lead from each component is connected, and the other leads are not connected to anything, then they are in series. But without a complete circuit, nothing "interesting" can happen -- no charge movement, no current flow, no voltage change,... nothing.

 

[ehild]

It was written in the problem that

"The battery is disconnected and the capacitors are rearranged in series."

Was this the original formulation of the problem? Or was there a hint that the series capacitors were connected to the battery again?

I agree that series and parallel connection of devices is defined with respect to the terminals of the resultant device. If both ends of those capacitors are connected they can only be connected into a circuit as parallel capacitors but not as series ones.

The polarity does not matter. Two batteries are in series either like terminals are connected or opposite ones (and the other terminals are free) and they are parallel either a positive terminal of one of them is connected to the positive one of the other battery, and negative to negative one, or the positive terminals are connected to the negative ones. The same is true for the capacitors. The charge is irrelevant.

ehild