vega32
- 2
- 0
Hi all,
I've got a question that came up while while carrying a sofa up the stairs. Is there a way that one could calculate whether or not the sofa (for the sake of simplifying, let's say that we're actually carrying a block -that wouldn't be far from the truth, given that the sofa remains in the cardboard container) would fit through the perpendicular bends in the stairway? OK, if the sofa is obviously not going to fit through, there is little point of even breaking a sweat doing the math, but nevertheless...
When one carries a sofa, the last resort at going through the bends is to lift the sofa up, so the longest side is facing up. Even if I disregard the height of the staircase, I still can't figure out the answer.
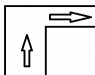
And too spice things up a bit, let's say that the staircase's width is wider before and narrower after the bend like in the attached picture.
I'd really appreciate your help.
Thanks!
I've got a question that came up while while carrying a sofa up the stairs. Is there a way that one could calculate whether or not the sofa (for the sake of simplifying, let's say that we're actually carrying a block -that wouldn't be far from the truth, given that the sofa remains in the cardboard container) would fit through the perpendicular bends in the stairway? OK, if the sofa is obviously not going to fit through, there is little point of even breaking a sweat doing the math, but nevertheless...
When one carries a sofa, the last resort at going through the bends is to lift the sofa up, so the longest side is facing up. Even if I disregard the height of the staircase, I still can't figure out the answer.
And too spice things up a bit, let's say that the staircase's width is wider before and narrower after the bend like in the attached picture.
I'd really appreciate your help.
Thanks!