Center of Mass coordinates Question

AI Thread Summary
The discussion focuses on calculating the center of mass coordinates for a system of four masses connected by rods. The formula used is Xc.m = ΣΔm x, where the individual masses and their distances from the origin are considered. The calculated x-coordinate of the center of mass is 16.24 cm. Participants seek guidance on determining both the x and y coordinates based on the provided diagram. The conversation emphasizes the need for clarity in applying the center of mass equations to solve the problem accurately.
AJDangles
Messages
48
Reaction score
0

Homework Statement



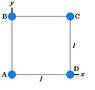
Four masses are connected by 17.4 cm long, massless, rigid rods. If massA=105.0 g, massB=231.0 g, massC=204.0 g, and massD=248.0 g, what are the coordinates of the center of mass if the origin is located at mass A?
See attached picture.

Homework Equations



Xc.m = \sumΔm x

The Attempt at a Solution



Xc.m = (0*105)+(248*17.4)+(204*17.4)+(231*17.4)/788
=16.24

How do you find the x and y coordinates?
 
Physics news on Phys.org
Here is the picture.
 

Attachments

  • Untitled.jpg
    Untitled.jpg
    4.7 KB · Views: 466

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Center of mass and momentum- A question about systems
Replies
25
Views
1K
Center of mass and rotation question
Replies
4
Views
6K
Displacement of Center of Mass Problem
Replies
3
Views
3K
Center of mass of two connected different density blocks
Replies
8
Views
4K
Center of Mass (Subtraction over addition)
Replies
7
Views
3K
Period of a physical pendulum with a pivot at its center
Replies
3
Views
3K
Center of Mass of Three Beads Equation
Replies
1
Views
8K
Finding the center of mass of a system
Replies
5
Views
4K
Center of Mass for a cubical box with a missing top
Replies
2
Views
14K
Rotation of a Rigid Body: Finding Center of Mass and Moment of Inertia
Replies
9
Views
2K

Hot Threads

Recent Insights

Back
Top