Center of mass of an inclined triangle

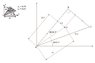
[Karol]

Homework Statement

Where's the COM

Homework Equations

The COM of a right triangle is a third of an edge apart of the right angle vertex

The Attempt at a Solution

Edge AC: $\frac{50}{\cos 20^0}=53.2$
Two thirds of edge AB: $\frac{53.2\cdot 30^0\cdot 2}{3}=30.7$
One third of edge BC: $\frac{53.2\cdot \sin 30^0}{3}=8.9$
Edge AO: $\sqrt {8.9^2+30.7^2}=32$
$$\cos \alpha=\frac{30.7}{32}\rightarrow \alpha=16.1^0$$
$$\beta=(30^0-\alpha)+20^0=33.9^0$$
Now i refer to drawing B:
$$x_{COM}=26.5 \surd,\ y_{COM}=17.8 \otimes$$

 

[paisiello2]

Are you trying to say that the value for xCOM is correct but yCOM is wrong?

yCOM is suppose to be = 14.4?

Now why aren't you taking the intersection of the medians to determine the point O which is the COM?

 

[ehild]

Homework Statement

Where's the COM

Homework Equations

The COM of a right triangle is a third of an edge apart of the right angle vertex

Your result is correct, but it would be easier to use the formula in the link, after having determined the coordinates of the vertexes.

http://www.mathopenref.com/coordcentroid.html

 

[Karol]

Thanks