Centre of Gravity of Multiple Crates

[joe465]

Homework Statement

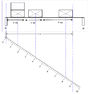
After a period of time the frame contains four crates.
Calculate the distance of the centre of gravity from the support A.

Homework Equations

The weight is 200KG per crate

The Attempt at a Solution

I know how to calculate the centre of gravity but this problem is stupid. There is an image attached to aid in understanding. It said on the previous question that the frame was 14m long. The first crate doesn't appear to begin at the start and looks as though it ends at 2m, so how far is it? Would i have to take this distance into consideration or should i just calculate the centre of gravity between the first 2 boxes and then add 2m to the final answer since it wants the distance from A. SHould i class the crates as being to the end of each arrow so it would make the first two boxes 2m apart and the last one 5m from the previous one?

I worked out the COG between first 2 was 0.67m to the right of the first one.
Then Since i worked out 0.67m i add that onto the 5m distance between the second and last one.
I worked out the overall centre of gravity being 1.4175m which i gather is from the end of the first boxes.
Add 2m since the distance to the first box is two to give 3.4175m from A.

Is this correct?

Thanks, in advanced

 

[gneill]

The figure is definitely very sloppy. If they're going to give you such vague information then I think you would be justified in making certain approximations.

I would be tempted to use an old drafting trick to lay a scale over the drawing and read off the centers of the crates measured from a chosen origin. So suppose that "A" on the diagram is that reference point, and it lies more or less along the center of the support at A. Take a centimeter rule and lay it at an angle on the diagram so that the 9cm mark aligns with a vertical drawn through the 2 + 2 + 5 = 9m distance indicated on the diagram. Drop verticals from the centers of the crates to the ruler and read off the distances. The scale is 1m = 1cm.

 

[joe465]

Thanks for your reply, i emailed my tutor about this and he said it was a typo and that 'Dimensions should refer to centre line of crates' so i guess my answer is correct?

 

[gneill]

Now that you know how the measurements actually pertain to the crates, why don't you work the problem again, showing your calculations.

 

[joe465]

First calculate the centre of gravity between the first two crates:

400x=200(2-x)
=400-200x
400x+200x=400
600x=400
x=400/600
x=0.67m (right of first crate)

Now i can recalculate the system by considering the mass of the first pair of objects as
being concentrated at this point.

600x=200(5.67-x)
=1134-200x
600x+200x=1134
800x=1134
x=1134/800
x=1.4175m

This gives 1.4175m to the right of the first crate. The first crate is 2m from A so:

1.4175m + 2m = 3.4175m to the right of A

Thanks, i hope this is right

 

[gneill]

I think you'll have to be more careful about calculating the distance between the center of mass of the first pair and the third crate. Also take more care with placing the absolute location of these centers of mass. A detailed diagram might help.

Alternatively, you should know that you can calculate the center of mass of the whole collection all in one go if you use the appropriate formula!

COM = \frac{\Sigma m_i d_i}{\Sigma m_i}
Where the m_i are the individual masses and the d_i are the distances from the reference point.

 

[joe465]

Would you say this was correct? This was the only method showing to me in the course so don't know the other way.

 

[gneill]

Would you say this was correct? This was the only method showing to me in the course so don't know the other way.

I would say that it is NOT correct. I think you lost track of some relative positions during your calculations.

A detailed diagram labeled with all the various distances would probably sort it out.

 

[joe465]

Thanks, i can't see where i am going wrong and I drew diagrams. I've attached a couple which i did in paint, not the best, the ones i did properly were on paper.

Just realized when i combined the masses i took the distance from the first one which was 0.67 and not the distance from the second one which is 1.33m.

so now the working out for the distance between final one is:

600x=200(6.33-x)
600x=1266-200x
600x+200x=1266
800x=1266
x=1266/800
x=1.5825

Does this mean the centre of gravity is 1.5825m to the right of the middle crate?
Which would give a total of 5.5825m to the right of A.

Or is it 1.5825+0.67+2=4.2525

I don't undertsand what is happening when combining the masses, where is the position are they in after they have been combined?
Is it on the previously worked COG or does it stay the same, how come i have to add the distance when there combined?
Absolutely lost now and getting more and more pissed off with ICS for there appauling teaching material.

 

[gneill]

When you find the center of gravity of two objects, you replace them both with a new point mass at the location of their center of gravity. When you do so you should make sure to locate it in terms of its distance from your reference point (point A in this case), not just with respect to one or the other of the original objects.

In the above diagram, the final COM will be located 2m + d1 + d3 to the right of A.

 

[joe465]

Ah brilliant, thankyou that has just cleared things up a lot more, the answer should be:

2m+0.67m+1.5825m=4.2525m from A