badaboom
- 23
- 0
Homework Statement
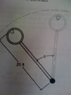
A centrifuge used for astronaut training starts moving from rest with a velocity Vi=8.5t[ft/sec]. It is know that a person loses consciousness when experiences an acceleration in the order of 10g. determine:
a)how long can hold the astronaut in the centrifuge before losing consciousness
b)the velocity of the astronaut
c)the normal and tangential acceleration of the astronaut
Homework Equations
normal acceleration = V2/20
tangential acceleration = v.
V12 =Vo2 + 2(tang. acceleration) * (s1-s0)
The Attempt at a Solution
I got the normal acceleration, (3.6125), but I don't know how to get the tangential acceleration since I don't have an initial OR final position. Any help?