Centripetal acceleration of a vehicle on banked circular arc

[Zatman]

Homework Statement

A van is moving on a horizontal circular bend in the road of radius 75m. The bend is banked at arctan(1/3) to the horizontal. The maximum speed at which the van can be driven around the bend without slipping is 25m/s. Calculate the coefficient of friction between the road surface and the tyres of the van.

Homework Equations

centripetal force = mv²/r
Friction ≤ μR

The Attempt at a Solution

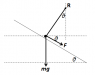
See attached diagram. At the maximum speed F=μR. Resolving perpendicular to the plane gives:

R = mgcosθ
∴ F = μmgcosθ

Resolving in a direction perpendicular to the weight gives:

Rsinθ + Fcosθ = mv²/r
mgsinθcosθ + μmgcos²θ = mv²/r

Solving for μ gives:

μ = [(v²/r)-gsinθcosθ]/[gcos²θ]

And substituting the values gives μ=0.61. This is apparently incorrect (the answer should be μ=0.40). I cannot see what I have done wrong.

Any hints would be greatly appreciated!

 

[haruspex]

R = mgcosθ

That would be true if there were no net acceleration perpendicular to the surface. But you know there is a net centripetal acceleration, and that is not parallel to the surface, therefore it has a component perpendicular to the surface.
Try resolving vertically instead.

 

[Zatman]

Ah, yes that makes sense. I got 0.40 now.

Thank you!