Centripetal Force of a tied ball

[Touchme]

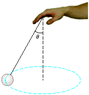
A 0.50 kg ball that is tied to the end of a 1.0 m light cord is revolved in a horizontal plane with the cord making a 30° angle, with the vertical (See Fig. P7.52.)

I managed to get my answer down to solving for theta however I don't know how to do the math:

I solved for T = mg / cos(x)
The Fc is = Tsin(x) = (mg)[tan(x)]
(mg)[tan(x)] = (mv^2) / r
R (radius) = 1sin(x)

The following equation is where I am stumped...
sin^2(x) / cos(x) = 8 / 4.9

 

[rsk]

Are you trying to find the speed?

Calculate Fc from Tsin(x) = (mg)[tan(x)]

Then calculate r, and you can find v.

I don't understand why you're stumped at that point, since you know what x is.

 

[Touchme]

sorry for not clarifying my question. I am trying to solve for x. The question is: If, instead, the ball is revolved so that its speed is 4.0 m/s, what angle does the cord make with the vertical?

 

[rsk]

OK - sorry for delay - site wouldn't let me post

sin^2(x) / cos(x) = 8 / 4.9

Gives you 4.9 sin^2 x = 8 cos^2 x

Remember sin^2 x = (1 - cos^2 x) - substitute this and you should be able to solve for cos x (might be a quadratic you have to solve)

 

[Touchme]

thank you so much.