Change in the kinetic energy of a car driving up a hill

[hello478]

Homework Statement

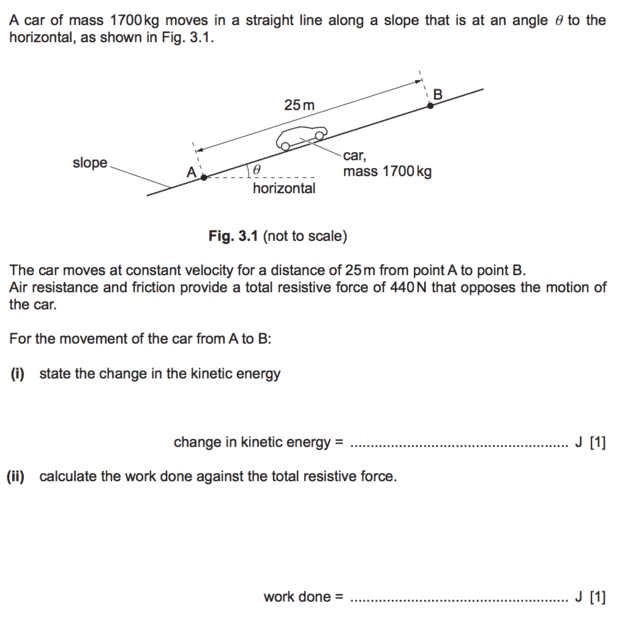
mentions below in picture

Relevant Equations

energy equations
and work done = f*d moved in direction of force

part i)
i did 1/2 * 1700 * v^2
i dont know what v is...
so how do i solve it?

part ii)
i calculated it correctly by 440*25
please explain in detail why i used 440?

and part d)
i did 1.7*10^4 = 48000/t
my t= 2.82 s
but correct answer is 3.5s

 

[Nugatory]

i dont know what v is...

You aren't being asked to calculate the kinetic energy, you are being asked how much it changes. You don't need the value of $v$ to perform that calculation.

please explain in detail why i used 440?

You are being asked to calculate the work done against the resistive force. What is that resistive force?

and part d)...

The work being done against the resistive force is not the only work that has to be done to get the car up the slope. Find the work that you haven't counted, include it, see what you get.

 

[hello478]

so for the first one
change in KE =0

resistive force is 440 so thats why we use it

and for part d
the total energy would be
gpe + the work done against resistive force
so 48000+440*25 / 17000
so time = 3.47 which is almost equal to 3.5
please tell me if im wrong
and thank you so much for your answer

 

[Nugatory]

Seems about right.