amind
- 36
- 4
Problem:
Consider two parallel and large sheets with a surface area
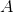 . One has a charge
. One has a charge
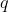 and the other is uncharged.
and the other is uncharged.
What would be the electric fields on the three regions as divided by the sheets ?
General solution to problems like as told by my teacher:
Using this principle, it is trivial to find a solution to this problem, distribution of charge:
The surface charge densities and thus the electric field dictated by this distribution is indeed the correct answer.
However, I really don't understand how/why this method works and my naive attempt at solving this problem comes out to be very wrong.
Here's my attempt:
The charge on one sheet would induce some charge of opposite polarity on the opposite end. I recall a similar situation where two conducting sheets have opposite charges, the charges are concentrated only on the inner surface resulting in 0 electric fields outside the sheets. Thus, I reason that the charge on the outer surfaces of both the sheets in this case would be 0, and on the inner surfaces it would be
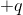 and
and
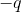 respectively.
respectively.
So, someone please help, where did I go wrong ? How (or should I say 'Why') does my teacher's rule follow ?
Consider two parallel and large sheets with a surface area
Code:
q
| |
| |
| |
| |
| |General solution to problems like as told by my teacher:
Find the sum of the charges on all of the sheets, and assign half of the net charge to the two extreme surfaces, then working you way from one side, assign charges on each surface such that two opposite surfaces have charges of equal magnitude but different sign, and that the sum of charges on both the surfaces of a sheet is equal to the charge given to it in the problem.
Using this principle, it is trivial to find a solution to this problem, distribution of charge:
Code:
+q/2 +q/2 -q/2 +q/2
| |
| |
| |
| |
| |However, I really don't understand how/why this method works and my naive attempt at solving this problem comes out to be very wrong.
Here's my attempt:
The charge on one sheet would induce some charge of opposite polarity on the opposite end. I recall a similar situation where two conducting sheets have opposite charges, the charges are concentrated only on the inner surface resulting in 0 electric fields outside the sheets. Thus, I reason that the charge on the outer surfaces of both the sheets in this case would be 0, and on the inner surfaces it would be
So, someone please help, where did I go wrong ? How (or should I say 'Why') does my teacher's rule follow ?