Charge on capacitor connected between spheres

[Saitama]

Homework Statement

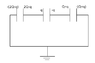
Two metallic spheres, each of radius R having charges 2Q and Q are joined through a capacitor of capacitance C as shown in the figure. Assuming R<<d, the charge on the capacitor long time after the key K is closed is:

(Ans: $\dfrac{Q}{2+\frac{4\pi \epsilon_0 R}{C}}$)

Homework Equations

The Attempt at a Solution

The final distribution of charges should be as shown in attachment 2.
From conservation of energy:
$$\frac{(2Q)^2}{2x}+\frac{Q^2}{2x}=\frac{(2Q-q)^2}{2x}+\frac{q^2}{2C}+\frac{(Q+q)^2}{2x}$$
where $x=4\pi \epsilon_0 R$.

Solving the above doesn't give me the right answer.

Any help is appreciated. Thanks!

 

[TSny]

The electrical potential energy is not conserved in this problem. Think about the final electric potential of each sphere and the capacitor.

 

[Saitama]

The electrical potential energy is not conserved in this problem.

Why the energy isn't conserved in this case?

Think about the final electric potential of each sphere and the capacitor.

Final electric potentials of the left sphere, capacitor and right spheres are $\frac{k(2Q-q)}{R}$, $q/C$ and $\frac{k(Q+q)}{R}$ respectively but I don't see what to do with the potentials.

 

[TSny]

How does the potential difference between the spheres relate to the potential difference across the plates of the capacitor?

 

[Curious3141]

Why the energy isn't conserved in this case?

In any problem involving redistribution of charges in a circuit, it's not safe to assume conservation of electrical energy. There is always "hidden" dissipation of energy as heat or EM waves, even when a circuit has no apparent resistance.

You'll notice this when working problems where a fully charged capacitor is then connected across an uncharged capacitor. Charge is conserved but the sum of the final PEs is not the same as what was present before. Energy is apparently "lost".

Final electric potentials of the left sphere, capacitor and right spheres are $\frac{k(2Q-q)}{R}$, $q/C$ and $\frac{k(Q+q)}{R}$ respectively but I don't see what to do with the potentials.

At equilibrium, what can you say about the potential of the left sphere with respect to the left plate of the capacitor? And then about the potential of the right sphere with respect to the right plate of the capacitor? And about the potential difference across the capacitor plates?

 

[TSny]

Why the energy isn't conserved in this case?

There will be conversion of electric potential energy into other forms of energy such as Joule heating and radiation.

 

[Saitama]

How does the potential difference between the spheres relate to the potential difference across the plates of the capacitor?

At equilibrium, what can you say about the potential of the left sphere with respect to the left plate of the capacitor? And then about the potential of the right sphere with respect to the right plate of the capacitor? And about the potential difference across the capacitor plates?

I made the circuit shown in attachment for the final configuration.

By KVL, I get:
$$\frac{k(2Q-q)}{R}-\frac{q}{C}-\frac{k(Q+q)}{R}=0$$
Solving the above gives me the right answer but I guess there is a better way to get the above equation?

 

[Curious3141]

I made the circuit shown in attachment for the final configuration.

By KVL, I get:
$$\frac{k(2Q-q)}{R}-\frac{q}{C}-\frac{k(Q+q)}{R}=0$$
Solving the above gives me the right answer but I guess there is a better way to get the above equation?

What I did is exactly what I wrote. At equilibrium, each plate of the capacitor will have the same potential as the sphere it's connected to (otherwise charge will still move and it will not be a stable equilibrium state). Let the left sphere and left plate (positive as it gains charge) be at voltage $V_L$ and the right plate (negative as it loses charge) and right sphere be at voltage $V_R$.

Then the potential difference across the capacitor is $V_L - V_R$, which you can equate to $\frac{q}{C}$.

Plug in all your variables to replace the voltage terms and you have a simple equation that almost immediately gives you the required answer.

 

[Saitama]

What I did is exactly what I wrote. At equilibrium, each plate of the capacitor will have the same potential as the sphere it's connected to (otherwise charge will still move and it will not be a stable equilibrium state). Let the left sphere and left plate (positive as it gains charge) be at voltage $V_L$ and the right plate (negative as it loses charge) and right sphere be at voltage $V_R$.

Then the potential difference across the capacitor is $V_L - V_R$, which you can equate to $\frac{q}{C}$.

Plug in all your variables to replace the voltage terms and you have a simple equation that almost immediately gives you the required answer.

Understood, thanks a lot Curious and TSny!