Charge on Cylinder Shell: Q1 + Q2

[RoyalFlush100]

Homework Statement

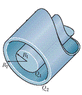
The figure is a section of a conducting rod of radius R1 = 1.60 mm and length L = 11.30 m inside a thin-walled coaxial conducting cylindrical shell of radius R2 = 10.5R1 and the (same) length L. The net charge on the rod is Q1 = +3.67 × 10-12 C; that on the shell is Q2 = -2.04Q1.

What is the charge on the interior and exterior surface of the shell?

Picture inserted below.

Homework Equations

I have no idea.

The Attempt at a Solution

I don't even know how to start this. I know the answer of the charge on the exterior is the sum of Q1 and Q2, but I don't know how where the answer came from.

 

[BvU]

Hello RF,
Guidelines don't like 'dunno' but I'll give you a hint: what about the $\vec E$ field between inner and outer R2 ? And: learn about Gauss already ?