utkarshakash
Gold Member
- 852
- 13
Homework Statement
Two particles have equal masses m and electric charges of equal magnitude and opposite sign (+q and –q). The particles are held at rest in uniform magnetic field B. The direction of the field is perpendicular to the line connecting the charges. The particles are released simultaneously. What is the minimum initial separation L that allows the particles not to collide after they are released? Neglect the effects of gravity.
The Attempt at a Solution
Let the distance of closest approach be d.
Applying conservation of energy,
\dfrac{-kq^2}{L} = mv^2 - \dfrac{kq^2}{d}
At distance of closest approach,
Fe=Fb
vd^2=kq/B
But it looks like I will need one more equation. If the trajectory of the particles were circular, I could have applied the formula r=mv/qB but this isn't the case here.
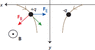
 . Have to rethink this one.
. Have to rethink this one.