Charges betweenand outside parallel sheets

[Linus Pauling]

1. You've hung two very large sheets of plastic facing each other with distance d between them, as shown in the figure . By rubbing them with wool and silk, you've managed to give one sheet a uniform surface charge density n_1 = -n_o and the other a uniform surface charge density n_2 = 3n_o .

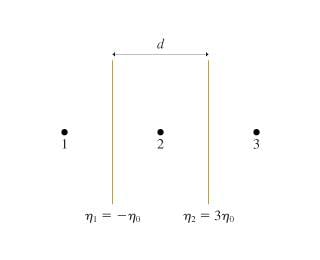
What is the field vector at each point? Give answer as a multiplier of n_o/epsilon_o.



2. E_cap = n/epsilon_o



3. So, for an ideal capacitor, E in between the two sheets is simply n/epsilon_o, and is zero outside because E_+ and E_- or of equal magnitude but opposite sign. So in this case, is the multiplier 4 for point 2, -2 for point 1, and 2 for point 3?

 

[kuruman]

Draw appropriate Gaussian surfaces and use Gauss's Law to see what is happening.

 

[netheril96]

The electric field given by a uniformly charged infinit plane is given by
$$\[<br /> E = \frac{\sigma }{{2\varepsilon _0 }}<br /> \]$$
This can be derived from Gauss' law

 

[kuruman]

The electric field given by a uniformly charged infinit plane is given by
$$\[<br /> E = \frac{\sigma }{{2\varepsilon _0 }}<br /> \]$$
This can be derived from Gauss' law

And how does it apply to the current situation?

 

[Linus Pauling]

Actually, we haven't covered Gauss' Law in class yet. Should I just read ahead to make my life easier?

 

[collinsmark]

I suggest against using any capacitor specific equations for this problem. The reason is those equations were derived assuming that there is an equal and opposite charge on each plate. 'Doesn't really apply here. Here, you should use the similar equation for a single plate (which is where the equation for the capacitor was derived from, btw.) which is

$$E= \frac{\sigma} {2 \epsilon _0}$$,

where $$\sigma$$ is the surface charge density.

I suggest working with each plate individually and using superposition to find the end result. This can be done separately for each point.

 

[netheril96]

And how does it apply to the current situation?

Just use superpositon principle
I think you should read Gauss' law in advance to make your life easier